
����Ŀ����ͼ�٣���һ��ֱ�����ǰ����ͬһ��ֱ��AB�ϣ����С�ONM=30�㣬��OCD=45�㣮
��1����ͼ���е����ǰ�OMN��BA�ķ���ƽ����ͼ�ڵ�λ�ã�MN��CD�ཻ�ڵ�E�����CEN�Ķ�����
��2����ͼ���е����ǰ�OMN�Ƶ�O����ʱ�뷽����ת����ͼ�ۣ�����CON=5��DOMʱ��MN��CD�ཻ�ڵ�E�������ж�MN��BC��λ�ù�ϵ�������CEN�Ķ���
��3����ͼ���е����ǰ�OMN�Ƶ�O��ÿ��5����ٶȰ���ʱ�뷽����תһ�ܣ�����ת�Ĺ����У����ǰ�MON�˶������ֱ��MNǡ����ֱ��CDƽ�У�
��4������ͼ��λ�õ��������ǰ�ͬʱ�Ƶ�O��ʱ����ת���ٶȷֱ�ÿ��20���ÿ��10�㣬������һ�����ǰ�ص���ʼλ��ʱ���������ǰ�ͬʱֹͣת�������� 9 ����OC���ON���ഹֱ����ֱ��д���𰸣�

���𰸡���1��105�㣻��2��135�㣻��3�����ǰ�MON�˶�15���51���ֱ��MNǡ����ֱ��CDƽ�У���4��9.
��������
�����������1�����������ε��ڽǺͶ�����ʽ���㼴�ɵý⣻
��2�����MN��OD��Ȼ�����ͬλ����ȣ���ֱ��ƽ���жϳ�MN��BC���ٸ�����ֱ��ƽ�У�ͬ���ڽǻ������
��3����������������ת�ǣ��ٸ���ʱ��=��ת�����ٶȼ��㼴�ɵý⣮
��4�������ת�ĽǶȲ�ٸ���ʱ��=��ת�Dz����ٶȲ���㼴�ɵý⣮
�����������1���ڡ�CEN�У���CEN=180��-30��-45��=105�㣻
��2����ͼ�ڣ��ߡ�CON=5��DOM
��180��-��DOM=5��DOM��
���DOM=30��
�ߡ�OMN=60�㣬
��MN��OD��
��MN��BC��
���CEN=180��-��DCO=180��-45��=135�㣻
��3����ͼ�ۣ�MN��CDʱ����ת��Ϊ90��-��60��-45�㣩=75�㣬
��270��-��60��-45�㣩=255�㣬
���ԣ�t=75���5��=15�룬
��t=255���5��=51�룻
���ԣ�����ת�Ĺ����У����ǰ�MON�˶�15���51���ֱ��MNǡ����ֱ��CDƽ�У�
��4��MN��CDʱ����ת�ǵĽǶȲ���90�㣬
����90��£�20��-10�㣩=9��.


 �ܿ���ȫ��100��ϵ�д�
�ܿ���ȫ��100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ʽax=ay�����б��β���ȷ���ǣ�������
A.x=y
B.ax+1=ay+1
C.2ax=2ay
D.3��ax=3��ay
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���������ε�һ�߳�Ϊ4����һ�߳�Ϊ8����������������ε��ܳ�Ϊ �� ��
A. 16 B. 20 C. 20��16 D. 12
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCO�ı�OA��OC���������ϣ���B����Ϊ��6��6������������ABCO�Ƶ�C��ʱ����ת�Ƕ�����0��������90�������õ�������CDEF��ED���߶�AB�ڵ�G��ED���ӳ��߽��߶�OA�ڵ�H����CH��CG��
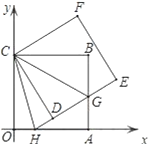
��1����֤����CBG�ա�CDG��
��2�����HCG�Ķ��������ж��߶�HG��OH��BG֮���������ϵ��˵�����ɣ�
��3������BD��DA��AE��EB�õ��ı���AEBD������ת�����У��ı���AEBD�ܷ�Ϊ���Σ�����ܣ��������H�����ꣻ������ܣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪����ABCD��AB=6��BC=8��E��F�ֱ���AB��BC���е㣬AF��DE�ཻ��I����BD�ཻ��H�����ı���BEIH�����Ϊ�� ��

A��![]() B��
B��![]() C��
C��![]() D��
D��![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵���У���ȷ�ĸ���Ϊ( )
������С������������������ѭ��С������������������������������С������������Ҳ�и���������������Ϊ�����������㡢����������
A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������������Գ�ͼ�Σ���Գ�����_______________________________��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com