
【题目】小明的妈妈在菜市场买回3斤萝卜、2斤排骨,准备做萝卜排骨汤,下面是爸爸妈妈的对话:
妈妈:“上个月萝卜的单价是![]() 元/斤,排骨的单价比萝卜的7倍还多2元”;
元/斤,排骨的单价比萝卜的7倍还多2元”;
爸爸:“今天,报纸上说与上个月相比,萝卜的单价上涨了25%,排骨的单价上涨了20%”
请根据上面的对话信息回答下列问题:
(1)请用含![]() 的式子填空:上个月排骨的单价是_________元/斤,这个月萝卜的单价是__________元/斤,排骨的单价是______________元/斤。
的式子填空:上个月排骨的单价是_________元/斤,这个月萝卜的单价是__________元/斤,排骨的单价是______________元/斤。
(2)列式表示今天买的萝卜和排骨比上月买同重量的萝卜和排骨一共多花多少元?(结果要求化成最简)
(3)当![]() =4,求今天买的萝卜和排骨比上月买同重量的萝卜和排骨一共多花多少元?
=4,求今天买的萝卜和排骨比上月买同重量的萝卜和排骨一共多花多少元?
【答案】(1)7a+2,125%a,8.4a+2.4;(2)(3.55a+0.8)元;(3)15元.
【解析】
(1)根据题意即可写出上个月排骨的单价、这个月萝卜的单价及排骨的单价;
(2)计算两次买的价钱,再相减即可求解;
(3)把a=4代入即可求解.
(1)∵上个月萝卜的单价是![]() 元/斤,排骨的单价比萝卜的7倍还多2元
元/斤,排骨的单价比萝卜的7倍还多2元
∴上个月排骨的单价是(7a+2)元/斤;
这个月萝卜的单价是(1+25%)a=125%a元/斤;
这个月排骨的单价是(1+20%)(7a+2)=(8.4a+2.4)元/斤
故填:7a+2,125%a,8.4a+2.4;
(2)今天买的萝卜和排骨花的钱数为3×125%a+2×(8.4a+2.4);
上个月买的萝卜和排骨花的钱数为3×a+2×(7a+2)
故今天买的萝卜和排骨比上月买同重量的萝卜和排骨一共多花的钱数为
[3×125%a+2×(8.4a+2.4)]-[ 3×a+2×(7a+2)]= 3.55a+0.8(元)
答:今天买的萝卜和排骨比上月买同重量的萝卜和排骨一共多花(3.55a+0.8)元;
(3)把![]() =4代入3.55a+0.8=3.55×4+0.8=15(元)
=4代入3.55a+0.8=3.55×4+0.8=15(元)
答:今天买的萝卜和排骨比上月买同重量的萝卜和排骨一共多花15元.


科目:初中数学 来源: 题型:
【题目】某商店销售A型和B型两种电脑,其中A型电脑每台的利润为400元,B型电脑每台的利润为500元.该商店计划再一次性购进两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的2倍,设购进A型电脑x台,这100台电脑的销售总利润为y元.
(1)求y关于x的函数关系式;
(2)该商店购进A型、B型电脑各多少台,才能使销售总利润最大,最大利润是多少?
(3)实际进货时,厂家对A型电脑出厂价下调a(0<a<200)元,且限定商店最多购进A型电脑60台,若商店保持同种电脑的售价不变,请你根据以上信息,设计出使这100台电脑销售总利润最大的进货方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
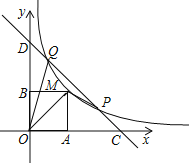
【题目】如图,在平面直角坐标系xOy中,函数y=![]() (m为常数,m>1,x>0)的图象经过点P(m,1)和Q(1,m),直线PQ与x轴,y轴分别交于C,D两点,点M(x,y)是该函数图象上的一个动点,过点M分别作x轴和y轴的垂线,垂足分别为A,B.
(m为常数,m>1,x>0)的图象经过点P(m,1)和Q(1,m),直线PQ与x轴,y轴分别交于C,D两点,点M(x,y)是该函数图象上的一个动点,过点M分别作x轴和y轴的垂线,垂足分别为A,B.
(1)求∠OCD的度数;
(2)当m=3,1<x<3时,存在点M使得△OPM∽△OCP,求此时点M的坐标;
(3)当m=5时,矩形OAMB与△OPQ的重叠部分的面积能否等于4.1?请说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC的三边长分别为3,4,5,△DEF的三边长分别为3,3x﹣2,2x+1,若这两个三角形全等,则x的值为( )
A. 2 B. 2或![]() C.
C. ![]() 或
或![]() D. 2或
D. 2或![]() 或
或![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=10厘米,∠B=∠C,BC=8厘米,点D为AB的中点,如果点P在线段BC上以3厘米/秒的速度由B点向C点运动,同时点Q在线段CA上由C点向A点运动,当一个点停止运动时,另一个点也随之停止运动,当点Q的运动速度为 时,能够在某一时刻使△BPD与△CQP全等.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,BC⊥AF于点C,∠A+∠1=90°.
(1)求证:AB∥DE;
(2)如图2,点P从点A出发,沿线段AF运动到点F停止,连接PB,PE.则∠ABP,∠DEP,∠BPE三个角之间具有怎样的数量关系(不考虑点P与点A,D,C重合的情况)?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新知识一般有两类:第一类是一般不依赖于其他知识的新知识,如“数”,“字母表示数”这样的初始性知识;第二类是在某些旧知识的基础上联系,拓展等方式产生的知识,大多数知识是这一类.
(1)多项式乘多项式的法则,是第几类知识?
(2)在多项式乘多项式之前,我们学习了哪些有关的知识?(写出三条即可)
(3)请你用已有的知识,从数和形两个方面说明多项式乘多项式法则,用(a+b)(a-b)来说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正方形ABCD,点P是对角线AC所在直线上的动点,点E在BC边所在直线上, PE=PB.
(1)如图1,当点E在线段BC上时,
求证:①PE=PD,②PE⊥PD.
简析: 由正方形的性质,图1中有三对全等的三角形,
即△ABC≌△ADC,_______≌_______,和_______≌______,由全等三角形性质,结合条件中PE=PB,易证PE=PD.要证PE⊥PD,考虑到∠ECD = 90°,故在四边形PECD中,只需证∠PDC +∠PEC=______即可.再结合全等三角形和等腰三角形PBE的性质,结论可证.

(2)如图2,当点E在线段BC的延长线上时,(1)中的结论是否成立?如果成立,请给出证明;如果不成立,请说明理由;

(3)若AB=1,当△PBE是等边三角形时,请直接写出PB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把ΔABC剪成三部分,边AB,BC,AC放在同一直线上,点O都落在直线MN上,直线MN∥AB.在ΔABC中,若∠AOB=125°,则∠ACB的度数为( )

A. 70°B. 65°C. 60°D. 85°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com