
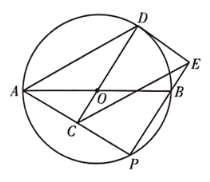
【题目】如图,AB是⊙O的直径,点P是AB下方的半圆上不与点A,B重合的一个动点,点C为AP的中点,连接CO并延长,交⊙O于点D,连接AD,过点D作⊙O的切线,交PB的延长线于点E,连接CE.
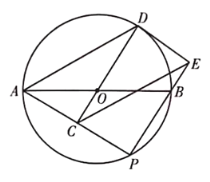
(1)求证:△DAC≌△ECP;
(2)填空:
①当∠DAP=______°时,四边形DEPC为正方形;
②在点 P的运动过程中,若⊙O的直径为10,tan∠DCE=![]() ,则AD=______.
,则AD=______.
【答案】(1)见解析;(2)①45,②![]() .
.
【解析】
(1)先由切线的性质得到∠CDE=90°,再利用垂径定理的推理得到DC⊥AP,接着根据圆周角定理得到∠APB=90°,于是可判断四边形DEPC为矩形,所以DC=EP,然后根据“SAS”判断△DAC≌△ECP;
(2)①利用四边形DEPC为矩形得到DE=PC=AC,则根据正方形的判定方法得DC=CP时,四边形DEPC为正方形,则DC=CP=AC,于是得到此时△ACD为等腰直角三角形,所以∠DAP=45°;
②先证明∠ADC=∠DCE,再在Rt△ACD中利用正切得到tan∠ADC=![]() ,则设AC=x,DC=2x,利用勾股定理得到AD=
,则设AC=x,DC=2x,利用勾股定理得到AD=![]() x,然后在Rt△AOC中利用勾股定理得到x2+(2x5)2=52,再解方程求出x即可得到AD的长.
x,然后在Rt△AOC中利用勾股定理得到x2+(2x5)2=52,再解方程求出x即可得到AD的长.
(1)证明:∵![]() 是
是![]() 的直径,
的直径,
∴![]() .
.
∵点![]() 为
为![]() 的中点,点
的中点,点![]() 为
为![]() 的中点,
的中点,
∴![]() 为
为![]() 的中位线,
的中位线,![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() .
.
∵![]() 是圆的切线,
是圆的切线,
∴![]() ,
,
∴四边形![]() 为矩形,
为矩形,
∴![]() .
.
又∵![]() ,
,![]() ,
,
∴![]() .
.
(2)解:①∵四边形DEPC为矩形,
∵DE=PC=AC,
∵当DC=CP时,四边形DEPC为正方形,
此时DC=CP=AC,
∴△ACD为等腰直角三角形,
∴∠DAP=45°;
②∵DE=AC,DE∥AC,
∴四边形ACED为平行四边形,
∴AD∥CE,
∴∠ADC=∠DCE,
在Rt△ACD中,tan∠ADC=![]() =tan∠DCE=
=tan∠DCE=![]() ,
,
设AC=x,则DC=2x,
∴AD=![]() ,
,
在Rt△AOC中,AO=5,OC=CDOD=2x5,
∴x2+(2x5)2=52,解得x1=0(舍去),x2=4,
∴AD=![]() .
.
故答案为①45;②![]() .
.


科目:初中数学 来源: 题型:
【题目】如图1,一张矩形纸片ABCD,其中AD=8cm,AB=6cm,先沿对角线BD折叠,点C落在点C′的位置,BC′交AD于点G.
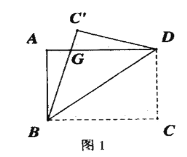
(1)求证:BG=DG;
(2)求C′G的长;
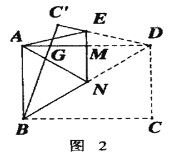
(3)如图2,再折叠一次,使点D与A重合,折痕EN交AD于M,求EM的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是⊙O的直径,以A为圆心,弦AB为半径画弧交⊙O于点C,连结BC交AD于点E,若DE=3,BC=8,则⊙O的半径长为( )

A.![]() B.5C.
B.5C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明对自己所在班级的50名学生平均每周参加课外活动的时间进行了调查,由调查结果绘制了频数分布直方图,根据图中信息回答下列问题:
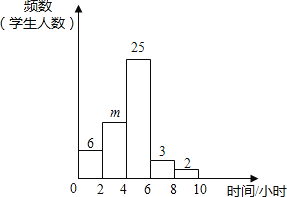
(1)求m的值;
(2)从参加课外活动时间在6~10小时的5名学生中随机选取2人,请你用列表或画树状图的方法,求其中至少有1人课外活动时间在8~10小时的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知E、F、G、H是四边形ABCD四边的中点,则四边形EFGH的形状为_____;如四边形ABCD的对角线AC 与BD的和为40,则四边形EFGH的周长为________.
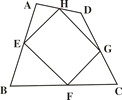
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①、图②,在给定的一张矩形纸片上作一个正方形,甲、乙两人的作法如下:
甲:以点A为圆心,AD长为半径画弧,交AB于点E,以点D为圆心,AD长为半径画弧,交CD于点F,连接EF,则四边形AEFD即为所求;
乙:作∠DAB的平分线,交CD于点M,同理作∠ADC的平分线,交AB于点N,连接MN,则四边形ADMN即为所求.


对于以上两种作法,可以做出的判定是( )
A.甲正确,乙错误B.甲、乙均正确
C.乙正确,甲错误D.甲、乙均错误
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l1∥l2,⊙O与l1和l2分别相切于点A和点B.点M和点N分别是l1和l2上的动点,MN沿l1和l2平移.⊙O的半径为1,∠1=60°.有下列结论:①MN=![]() ;②若MN与⊙O相切,则AM=
;②若MN与⊙O相切,则AM=![]() ;③若∠MON=90°,则MN与⊙O相切;④l1和l2的距离为2,其中正确的有( )
;③若∠MON=90°,则MN与⊙O相切;④l1和l2的距离为2,其中正确的有( )
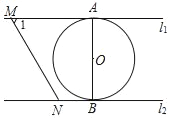
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,BA=BC,BD平分∠ABC.
(1)求证:四边形ABCD是菱形;
(2)过点D作DE⊥BD,交BC的延长线于点E,若BC=5,BD=8,求四边形ABED的周长.
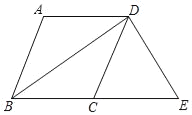
查看答案和解析>>
科目:初中数学 来源: 题型:
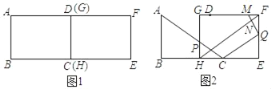
【题目】把两个全等的矩形ABCD和EFGH如图1摆放(点D和点G重合,点C和点H重合),点A、D(G)在同一条直线上,AB=6cm,BC=8cm.如图2,△ABC从图1位置出发,沿BC方向匀速运动,速度为1cm/s,AC与GH交于点P;同时,点Q从点E出发,沿EF方向匀速运动,速度为1cm/s.点Q停止运动时,△ABC也停止运动.设运动时间为t(s)(0<t<6).
(1)当t为何值时,CQ∥FH;
(2)过点Q作QM⊥FH于点N,交GF于点M,设五边形GBCQM的面积为y(cm2),求y与t之间的函数关系式;
(3)在(2)的条件下,是否存在某一时刻,使点M在线段PC的中垂线上?若存在,请求出t的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com