【题目】如图，在平面直角坐标系xOy中，A（-1，0），B（-3，-3），若BC∥OA，且BC=4OA.
（1）求点C的坐标；
（2）求△ABC的面积.
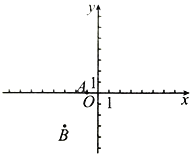
【答案】（1）（1，-3）或（-7，-3）（2）6
【解析】试题分析：（1）由已知条件得出BC=4，点C的纵坐标为-3，BM=3，分两种情况：①当点C在点B的右边时，CM=BC-BM=1，即可得出点C的坐标；
②当点C在点B的左边时，CM=BC+BM=7，即可得出点C的坐标；
（2）由三角形面积公式得出△ABC的面积=
BC×OM，即可得出结果．
试题解析：（1）如图所示：∵A（-1，0），
∴OA=1，
∵B（-3，-3），BC∥OA，且BC=4OA，
∴BC=4.
设C（x，-3），
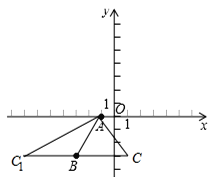
当点C在点B的右边时，此时x-(-3)=4，
解得x=1，
即C（1，-3）；
当点C在点B的左边时，此时-3-x=4，
解得x=-7，
即C（-7，-3）.
则点C的坐标为（1，-3）或（-7，-3）；
（2）△ABC的面积=BC×3=×4×3=6.
科目：初中数学 来源： 题型：
【题目】为了保护环境，某企业决定购买10台污水处理设备；现有A、B两种型号的设备，其中每台的价格、月处理污水量及年消耗费如下表：
A型 | B型 | |
价格（万元/台） | 12 | 10 |
处理污水量（吨/月） | 240 | 200 |
年消耗费（万元/台） | 1 | 1 |
经预算，该企业购买设备的资金不高于105万元。
（1） 请你设计该企业有几种购买方案；
（2）若该企业每月产生的污水量为2040吨，为了节约资金，应选择哪种购买方案？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】计算：
（1）（﹣a2）3+（﹣a3）2﹣a2a3；
（2）（3+a）（3﹣a）+a2；
（3）（x+y﹣3）（x+y+3）；
（4）（
）﹣2+（﹣2）3+|﹣3|﹣（π﹣3.14）0．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，△ABC在直角坐标系中，
（1）请写出△ABC各点的坐标；
（2）求出△ABC的面积；
（3）若把△ABC向上平移2个单位，再向右平移2个单位得到△A'B'C'，在图中画出△ABC变化位置，并写出A'、B'、C'的坐标.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知如图，四边形ABCD的四个顶点的坐标分别为A（0，0）、B（9，0）、C（7，5）、D（2，7）．
（1）试计算四边形ABCD的面积；
（2）若将该四边形各顶点的横坐标都加2，纵坐标都加3，其面积怎么变化？为什么？
查看答案和解析>>
科目：初中数学 来源： 题型：
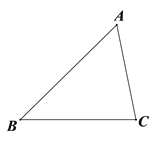
【题目】如图，△ABC.
（1）用直尺和圆规作∠A的平分线所在的直线
和边BC的垂直平分线
（要求：不写作法，保留画图痕迹）；
（2）设（1）中的直线
和直线
交于点P，过点P作PE⊥AB，垂足为点E，过点P作PF⊥AC交AC的延长线于点F.请探究BE和CF的数量关系，并说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在学习了二次根式后，小明同学发现有的二次根式可以写成另一个二次根式的平方的形式.
比如： 
.善于动脑的小明继续探究：
当
为正整数时，若
，则有
，所以
， 
.
请模仿小明的方法探索并解决下列问题：
（1）当
为正整数时，若
，请用含有
的式子分别表示
，得： 
， 
；
（2）填空： 
- 
；
（3）若
，且
为正整数，求
的值.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在如图所示的正方形网格中，每个小正方形的边长为1，格点三角形ABC（顶点是网格线的交点的三角形）的顶点A，C的坐标分别为（
， 
），（
， 
）．
（1）请在如图所示的网格平面内，作出平面直角坐标系；
（2）请作出
关于
轴对称的
；
（3）写出点
的坐标为___ __；
（4）△ABC的面积为__ _ ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图．下列三个条件：①AB∥CD，②∠B=∠C．③∠E=∠F．从中任选两个作为条件，另一个作为结论，编一道数学题，并说明理由．
已知：________；
结论：________；
理由：________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com