
【题目】如图,点O为直线AB上一点,∠AOC=110°,OM平分∠AOC,∠MON=90° 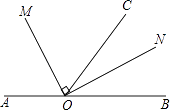
(1)求∠BOM的度数;
(2)ON是∠BOC的角平分线吗?请说明理由.
【答案】
(1)解:∵OM平分∠AOC,
∴∠AOM= ![]() ∠AOC=55°,
∠AOC=55°,
∴∠BOM=∠AOB﹣∠AOM=180°﹣55°=125°
(2)解:ON是∠BOC的角平分线.理由如下:
∵∠MON=90°,∠AOB=180°,
∴∠MOC+∠CON=90°,∠AOM+∠BON=90°,
又由(1)可知∠AOM=∠MOC,
∴∠CON=∠BON,
即ON是∠BOC的角平分线
【解析】(1)根据角的平分线的定义求得∠AOM的度数,然后根据邻补角的定义求得∠BOM的度数;(2)首先根据∠MON=90°,∠AOB=180°,得出∠MOC+∠CON=90°,∠AOM+∠BON=90°,又∠AOM=∠MOC,根据等角的余角相等即可得到ON是∠BOC的角平分线.
【考点精析】根据题目的已知条件,利用角的平分线和角的运算的相关知识可以得到问题的答案,需要掌握从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线;角之间可以进行加减运算;一个角可以用其他角的和或差来表示.


 快捷英语周周练系列答案
快捷英语周周练系列答案科目:初中数学 来源: 题型:
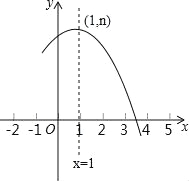
【题目】如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,n),且与x轴的一个交点在点(3,0)和(4,0)之间.则下列结论:
①a﹣b+c>0;
②3a+b=0;
③b2=4a(c﹣n);
④一元二次方程ax2+bx+c=n﹣1有两个不相等的实数根.
其中正确结论的个数是( )
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点O为直线AB上一点,过点O作射线OC,使∠BOC=120°,将有一30度角的直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.(图中∠OMN=30°,∠NOM=90°) 
(1)将图1中的三角板绕点O逆时针旋转至图2,使OM在∠BOC的内部,且恰好平分∠BOC,问直线ON是否平分∠AOC?请说明理由;
(2)将图1中的三角板绕点O按每秒6°的速度沿逆时针方向旋转一周,在旋转的过程中,第t秒时,直线ON恰好平分锐角∠AOC,求t;
(3)将图1中的三角板绕点O顺时针旋转至图3,使ON在∠AOC的内部,请探究:∠AOM与∠NOC之间的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①点A,B,C,D在同一直线上,AB=CD,作CE⊥AD,BF⊥AD,且AE=DF. 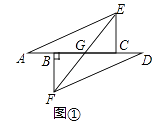
(1)证明:EF平分线段BC;
(2)若△BFD沿AD方向平移得到图②时,其他条件不变,(1)中的结论是否仍成立?请说明理由. 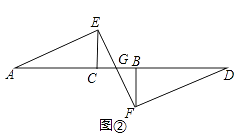
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算下列各题
(1)12+(﹣18)﹣(﹣7)﹣15
(2)3×(﹣2)﹣(﹣1)÷ ![]() ×(﹣3)
×(﹣3)
(3)﹣12010﹣ ![]() ×[2﹣(﹣3)2]
×[2﹣(﹣3)2]
(4)|﹣ ![]() |÷(
|÷( ![]() ﹣
﹣ ![]() )﹣(0.75﹣
)﹣(0.75﹣ ![]() ﹣
﹣ ![]() )×24.
)×24.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com