
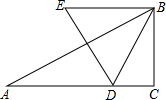
 如图,已知△ABC,∠C=90°,∠A=30°,AC=$\sqrt{3}$,动点D在边AC上,以BD为边作等边△BDE(点E、A在BD的同侧),在点D从点A移动至点C的过程中,点E移动的路线为( )
如图,已知△ABC,∠C=90°,∠A=30°,AC=$\sqrt{3}$,动点D在边AC上,以BD为边作等边△BDE(点E、A在BD的同侧),在点D从点A移动至点C的过程中,点E移动的路线为( )| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | $\frac{π}{3}$ | D. | $\frac{2π}{3}$ |
分析 作EF⊥AB垂足为F,连接CF,由△EBF≌△DBC,推出点E在AB的垂直平分线上,在点D从点A移动至点C的过程中,点E移动的路线和点D运动的路线相等,由此即可解决问题.
解答 解:如图,作EF⊥AB垂足为F,连接CF.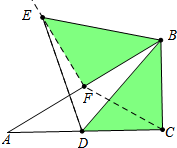
∵∠ACB=90°,∠A=30°,
∴∠ABC=60°,
∵△EBD是等边三角形,
∴BE=BD,∠EBD=60°,
∴∠EBD=∠ABC,
∴∠EBF=∠DBC,
在△EBF和△DBC中,
$\left\{\begin{array}{l}{∠EFB=∠BCD=90°}\\{∠EBF=∠DBC}\\{EB=BD}\end{array}\right.$,
∴△EBF≌△DBC,
∴BF=BC,EF=CD,∵∠FBC=60°,
∴△BFC是等边三角形,
∴CF=BF=BC,
∵BC=$\frac{1}{2}$AB=,
∴BF=$\frac{1}{2}$AB,
∴AF=FB,
∴点E在AB的垂直平分线上,
∴在点D从点A移动至点C的过程中,点E移动的路线和点D运动的路线相等,
∴在点D从点A移动至点C的过程中,点E移动的路线为$\sqrt{3}$.
故选A.
点评 本题考查轨迹、等边三角形的性质、全等三角形的判定和性质等知识,解题的关键是添加辅助线构造全等三角形,正确找到点E的运动路线,属于中考常考题型.


 百年学典课时学练测系列答案
百年学典课时学练测系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在点O处测得远处动点P作匀速直线运动,开始位置在A点,一分钟后到达B点,再过一分钟到达C点,测得∠AOB=90°,∠BOC=30°,则tan∠OAB=( )
如图,在点O处测得远处动点P作匀速直线运动,开始位置在A点,一分钟后到达B点,再过一分钟到达C点,测得∠AOB=90°,∠BOC=30°,则tan∠OAB=( )| A. | $\frac{3}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{2\sqrt{3}}}{3}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,矩形ABCD中,AB=9,AD=3.点E从D向C以每秒1个单位的速度运动,以AE为一边在AE的右下方作正方形AEFG,同时垂直于CD的直线MN也从C向D以每秒2个单位的速度运动,当经过2秒时,直线MN和正方形AEFG开始有公共点.
如图,矩形ABCD中,AB=9,AD=3.点E从D向C以每秒1个单位的速度运动,以AE为一边在AE的右下方作正方形AEFG,同时垂直于CD的直线MN也从C向D以每秒2个单位的速度运动,当经过2秒时,直线MN和正方形AEFG开始有公共点.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在矩形ABCD中,AB=5,BC=6,点E是AD上一点,把△BAE沿BE向矩形内部折叠,当点A的对应点A1恰落在∠ADC的平分线上时,DA1=2$\sqrt{2}$.
如图,在矩形ABCD中,AB=5,BC=6,点E是AD上一点,把△BAE沿BE向矩形内部折叠,当点A的对应点A1恰落在∠ADC的平分线上时,DA1=2$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 在一个边长不超过8厘米的大正方形ABCD中,如图所示,放入3张面积都是20平方厘米的小正方形纸片BEFG、OPNC、IQKJ,已知3张小正方形纸片盖住的总面积为44平方厘米,那么大正方形ABCD和小正方形BEFG的边长之比为( )
在一个边长不超过8厘米的大正方形ABCD中,如图所示,放入3张面积都是20平方厘米的小正方形纸片BEFG、OPNC、IQKJ,已知3张小正方形纸片盖住的总面积为44平方厘米,那么大正方形ABCD和小正方形BEFG的边长之比为( )| A. | 5:3 | B. | 3:2 | C. | 10:7 | D. | 8:5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
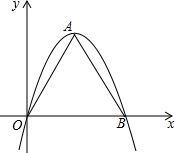 如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.
如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{7}{2}$ | B. | 3 | C. | $\frac{5}{2}$ | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com