
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
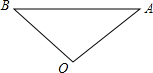 如图,爸爸从家(点O)出发,沿着等腰三角形AOB的边OA→AB→BO的路径去匀速散步,其中OA=OB.设爸爸距家(点O)的距离为S,散步的时间为t,则下列图形中能大致刻画S与t之间函数关系的图象是( )
如图,爸爸从家(点O)出发,沿着等腰三角形AOB的边OA→AB→BO的路径去匀速散步,其中OA=OB.设爸爸距家(点O)的距离为S,散步的时间为t,则下列图形中能大致刻画S与t之间函数关系的图象是( )| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,已知在Rt△ABC中,AB=AC=$\frac{3\sqrt{2}}{2}$,在△ABC内作第一个内接正方形DEFG;然后取GF的中点P,连接PD、PE,在△PDE内作第二个内接正方形HIKJ;再取线段KJ的中点Q,在△QHI内作第三个内接正方形…依次进行下去,则第2016个内接正方形的边长为($\frac{1}{2}$)2015.
如图,已知在Rt△ABC中,AB=AC=$\frac{3\sqrt{2}}{2}$,在△ABC内作第一个内接正方形DEFG;然后取GF的中点P,连接PD、PE,在△PDE内作第二个内接正方形HIKJ;再取线段KJ的中点Q,在△QHI内作第三个内接正方形…依次进行下去,则第2016个内接正方形的边长为($\frac{1}{2}$)2015.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图1,C地位于A,B两地之间,甲步行直接从C地前往B地;乙骑自行车由C地先回A地,再从A地前往B地(在A地停留时间忽略不计).已知两人同时出发且速度不变,乙的速度是甲的$\frac{5}{2}$倍,设出发xmin后甲、乙两人离C地的距离分别为y1m,y2m,图②中线段OM表示y1与x的函数图象.
如图1,C地位于A,B两地之间,甲步行直接从C地前往B地;乙骑自行车由C地先回A地,再从A地前往B地(在A地停留时间忽略不计).已知两人同时出发且速度不变,乙的速度是甲的$\frac{5}{2}$倍,设出发xmin后甲、乙两人离C地的距离分别为y1m,y2m,图②中线段OM表示y1与x的函数图象.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
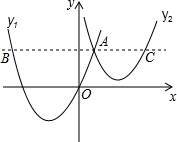 如图,抛物线y1=a(x+2)2+m过原点,与抛物线y2=$\frac{1}{2}$(x-3)2+n交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.下列结论:①两条抛物线的对称轴距离为5;②x=0时,y2=5;③当x>3时,y1-y2>0;④y轴是线段BC的中垂线.正确结论是①③④(填写正确结论的序号).
如图,抛物线y1=a(x+2)2+m过原点,与抛物线y2=$\frac{1}{2}$(x-3)2+n交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.下列结论:①两条抛物线的对称轴距离为5;②x=0时,y2=5;③当x>3时,y1-y2>0;④y轴是线段BC的中垂线.正确结论是①③④(填写正确结论的序号).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在平面直角坐标系中,O为坐标原点,A(-2,3),B(2,2).
在平面直角坐标系中,O为坐标原点,A(-2,3),B(2,2).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
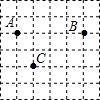 吴磊在如图所示的某校的平面示意图中建立平面直角坐标系,若表示图书馆位置的点A和表示食堂位置的点B都在x轴上,且关于y轴对称,则表示教学楼位置的点C的坐标是( )
吴磊在如图所示的某校的平面示意图中建立平面直角坐标系,若表示图书馆位置的点A和表示食堂位置的点B都在x轴上,且关于y轴对称,则表示教学楼位置的点C的坐标是( )| A. | (1,-2) | B. | (-1,2) | C. | (-1,-2) | D. | (-1,-1) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
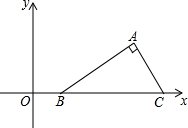 如图,在平面直角坐标系中Rt△ABC的斜边BC在x轴上,点B坐标为(1,0),AC=2,∠ABC=30°,把Rt△ABC先绕B点顺时针旋转180°,然后再向下平移2个单位,则A点的对应点A′的坐标为( )
如图,在平面直角坐标系中Rt△ABC的斜边BC在x轴上,点B坐标为(1,0),AC=2,∠ABC=30°,把Rt△ABC先绕B点顺时针旋转180°,然后再向下平移2个单位,则A点的对应点A′的坐标为( )| A. | (-4,-2-$\sqrt{3}$) | B. | (-4,-2+$\sqrt{3}$) | C. | (-2,-2+$\sqrt{3}$) | D. | (-2,-2-$\sqrt{3}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com