
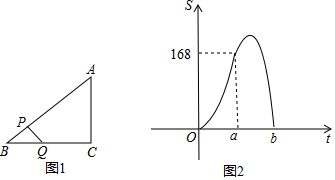
分析 (1)根据当点Q与点C重合时,S=168,即可得到t=4,进而得出BC的长以及点P、Q相遇的时间;
(2)由(1)可得,当0≤t<4时,S=$\frac{21}{2}{t}^{2}$,过Q作QE⊥AB于E,根据Rt△AEQ中,EQ=$\frac{4}{5}$(49-7t),即可得到S=-14t2+98t(4≤t≤7).
解答 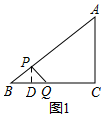 解:(1)如图1,由题可得,BP=5t,BQ=7t,
解:(1)如图1,由题可得,BP=5t,BQ=7t,
过P作PD⊥BC于D,则△PBD∽△ABC,
又∵AB:BC=5:4,
∴PD=$\frac{3}{5}$BP=3t,
∴S=$\frac{1}{2}$×7t×3t=$\frac{21}{2}{t}^{2}$,
∴当点Q与点C重合时,S=168,即168=$\frac{21}{2}{t}^{2}$,
解得t=4,(负值已舍去)
∴BC=4×7=28,a=4,
∴AC=$\frac{3}{4}$BC=21,AB=$\frac{5}{4}$BC=35,
∴点P、Q相遇的时间=$\frac{35+28+21}{5+7}$=7(s),
∴b=7,
故答案为:28,7;
(2)由(1)可得,当0≤t<4时,S=$\frac{21}{2}{t}^{2}$,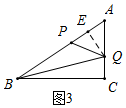
∵7×5=35,
∴两点在点A处相遇,
如图3,过Q作QE⊥AB于E,则△AQE∽△ABC,
∵AQ=21+28-7t=49-7t,
∴Rt△AEQ中,EQ=$\frac{4}{5}$AQ=$\frac{4}{5}$(49-7t),
∴S=$\frac{1}{2}$×5t×$\frac{4}{5}$(49-7t)=-14t2+98t(4≤t≤7),
综上所述,S关于t的函数关系式为S=$\left\{\begin{array}{l}{\frac{21}{2}{t}^{2}(0≤t<4)}\\{-14{t}^{2}+98t(4≤t≤7)}\end{array}\right.$.
点评 本题主要考查了动点问题的函数图象,解决问题的关键是理清图象的含义即会识图.通过看图获取信息,不仅可以解决生活中的实际问题,还可以提高分析问题、解决问题的能力.


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:初中数学 来源: 题型:解答题
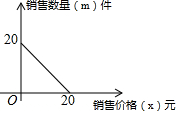 某商场以每件10元的价格购进一种商品,试销中发现,这种商品每天的销售量m(件)与每件的销售价x(元)满足一次函数,其函数图象如图所示.
某商场以每件10元的价格购进一种商品,试销中发现,这种商品每天的销售量m(件)与每件的销售价x(元)满足一次函数,其函数图象如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
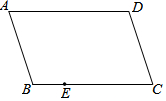 如图,ABCD是平行四边形,E是BC边上一点,只用一把无刻度的直尺在AD边上作点F,使得DF=BE.画出满足题意的点F,并简要说明你的画图过程.
如图,ABCD是平行四边形,E是BC边上一点,只用一把无刻度的直尺在AD边上作点F,使得DF=BE.画出满足题意的点F,并简要说明你的画图过程.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 “龟兔赛跑”的故事同学们都非常熟悉,图中的线段和折线OABC表示“龟兔赛跑”时路程与时间的关系,请你根据图中给出的信息,下列说法:
“龟兔赛跑”的故事同学们都非常熟悉,图中的线段和折线OABC表示“龟兔赛跑”时路程与时间的关系,请你根据图中给出的信息,下列说法:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| x | -3 | -2 | -1 | 1 | 2 | 3 |
| y=-x+1 | 4 | 3 | 2 | 0 | -1 | -2 |
| y=$\frac{k}{x}$ | $\frac{2}{3}$ | 1 | 2 | -2 | -1 | -$\frac{2}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
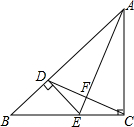 已知,如图,△ABC中,AC=BC,∠C=90°,AE平分∠BAC交BC于E,过E作ED⊥AB于D,连接DC交AE于F,其中BD=1,下列结论:①DC⊥AE;②AB=2+$\sqrt{2}$;③CD•AE=2$\sqrt{2}$+2;④$\frac{AE}{CD}$=2:1,其中正确的结论是①②③.
已知,如图,△ABC中,AC=BC,∠C=90°,AE平分∠BAC交BC于E,过E作ED⊥AB于D,连接DC交AE于F,其中BD=1,下列结论:①DC⊥AE;②AB=2+$\sqrt{2}$;③CD•AE=2$\sqrt{2}$+2;④$\frac{AE}{CD}$=2:1,其中正确的结论是①②③.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
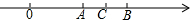 如图,数轴上点C和点B分别表示2和$\sqrt{5}$,若点C是AB的中点,点A表示的实数为( )
如图,数轴上点C和点B分别表示2和$\sqrt{5}$,若点C是AB的中点,点A表示的实数为( )| A. | 2-$\sqrt{5}$ | B. | 4-$\sqrt{5}$ | C. | -$\sqrt{5}$ | D. | $\sqrt{5}$-2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com