
 在平面直角坐标系中,对于任意一点P(x,y),我们做以下规定:d(P)=|x|+|y|,称d(P)为点P的坐标距离.
在平面直角坐标系中,对于任意一点P(x,y),我们做以下规定:d(P)=|x|+|y|,称d(P)为点P的坐标距离.分析 (1)根据d(P)=|x|+|y|,即可求得点P的坐标距离d(A);
(2)①证明:如图1,过点A作AE⊥y轴于E,作CF⊥y轴于F,则∠CFO=∠OEA=90°,设A(b,a),C(n,m),则|a|=OE,|b|=AE,|m|=OF,|n|=CF,根据相似三角形的性质得到$\frac{OC}{AO}$=$\frac{CF}{OE}$=$\frac{OF}{AE}$=1,求得$\frac{CF+OF}{OE+AE}$=1,于是得到$\frac{|n|+|m|}{|a|+|b|}$=1,即可得到结论;
②如图1所示,过点B作BG⊥CF,交FC的延长线于G,交x轴于H,则GF=OH,GH=OF,∠G=∠AEO=90°,根据余角的性质得到∠BCG=∠COF,根据全等三角形的性质得到OE=BG,AE=CG,由图可得,d(A)=OE+AE,d(C)=OF+CF,d(B)=BH+OH=BH+GF,根据已知条件得到OE+AE+OF+CF=BH+GF+2,求得OF=1,解直角三角形得到CF=$\sqrt{3}$,由于$\frac{OC}{AO}$=$\frac{CF}{OE}$=$\frac{OF}{AE}$=1,求得BG=$\sqrt{3}$,CG=1,于是得到结论.
解答 解:(1)∵点P(3,-4),
∴点A的坐标距离d(P)=|3|+|-4|=3+4=7;
(2)①证明:如图1,过点A作AE⊥y轴于E,作CF⊥y轴于F,则∠CFO=∠OEA=90°,
设A(b,a),C(n,m),则|a|=OE,|b|=AE,|m|=OF,|n|=CF,
∵在正方形ABCO中,∠AOC=90°,
∴∠AOE+∠COF=90°,
又∵∠AOE+∠EAO=90°,
∴∠COF=∠OAE,
∴△CFO∽△OEA,
∴$\frac{OC}{AO}$=$\frac{CF}{OE}$=$\frac{OF}{AE}$=1,
∴$\frac{CF+OF}{OE+AE}$=1,即$\frac{|n|+|m|}{|a|+|b|}$=1,
即|a|+|b|=|m|+|n|,
∴d(A)=d(C);
②如图1所示,过点B作BG⊥CF,交FC的延长线于G,交x轴于H,则GF=OH,GH=OF,∠G=∠AEO=90°,
∵∠BCO=90°=∠CFO,
∴∠BCG+∠FCO=∠COF+∠FCO=90°,
∴∠BCG=∠COF,
∵∠COF=∠OAE,
∴∠BCG=∠OAE,
∵四边形ABCO是正方形,
∴CB=AO,
在△BCG和△OAE中,$\left\{\begin{array}{l}{∠BCG=∠OAE}\\{∠G=∠AEO}\\{BC=AO}\end{array}\right.$,
∴△BCG≌△OAE(AAS),
∴OE=BG,AE=CG,
由图可得,d(A)=OE+AE,d(C)=OF+CF,d(B)=BH+OH=BH+GF,
∵d(A)+d(C)=d(B)+2,
∴OE+AE+OF+CF=BH+GF+2,
又∵BH=BG-GH=OE-OF,GF=CG+CF=AE+CF,
∴OE+AE+OF+CF=(OE-OF)+(AE+CF)+2,
∴即OF=2-OF,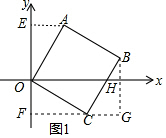
∴OF=1,
∵在Rt△COF中,CO=2,
∴CF=$\sqrt{3}$,
又∵$\frac{OC}{AO}$=$\frac{CF}{OE}$=$\frac{OF}{AE}$=1,
∴$\frac{\sqrt{3}}{OE}$=$\frac{1}{AE}$=1,即OE=$\sqrt{3}$,AE=1,
∴BG=$\sqrt{3}$,CG=1,
∴FG=CG+CF=1+$\sqrt{3}$=OH,BH=BG-OF=$\sqrt{3}$-1,
∴B(1+$\sqrt{3}$,$\sqrt{3}$-1).
点评 本题属于四边形综合题,主要考查了正方形的性质,相似三角形的判定与性质以及坐标与图形的性质的综合应用,解题时注意:坐标平面内点到x轴的距离与纵坐标有关,到y轴的距离与横坐标有关;距离都是非负数,而坐标可以是负数,在由距离求坐标时,需要加上恰当的符号.


科目:初中数学 来源: 题型:填空题
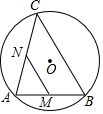 如图,AB是⊙O的弦,AB=5,点C是⊙O上的一个动点,且∠ACB=45°,若点M、N分别是AB、AC的中点,则MN长的最大值是$\frac{5\sqrt{2}}{2}$.
如图,AB是⊙O的弦,AB=5,点C是⊙O上的一个动点,且∠ACB=45°,若点M、N分别是AB、AC的中点,则MN长的最大值是$\frac{5\sqrt{2}}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
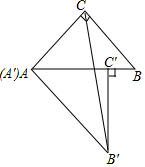 如图,将两个大小、形状完全相同的△ABC和△A′B′C′拼在一起,其中点A′与点A重合,点C′落在边AB上,连接B′C.若∠ACB=∠AC′B′=90°,AC=BC=3,则B′C的长为( )
如图,将两个大小、形状完全相同的△ABC和△A′B′C′拼在一起,其中点A′与点A重合,点C′落在边AB上,连接B′C.若∠ACB=∠AC′B′=90°,AC=BC=3,则B′C的长为( )| A. | 3$\sqrt{3}$ | B. | 6 | C. | 3$\sqrt{2}$ | D. | $\sqrt{21}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 将油滴入水中,油会浮在水面上 | |
| B. | 车辆随机到达一个路口,遇到红灯 | |
| C. | 如果a2=b2,那么a=b | |
| D. | 掷一枚质地均匀的硬币,一定正面向上 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某校学生会决定从三明学生会干事中选拔一名干事当学生会主席,对甲、乙、丙三名候选人进行了笔试和面试,三人的测试成绩如下表所示:
某校学生会决定从三明学生会干事中选拔一名干事当学生会主席,对甲、乙、丙三名候选人进行了笔试和面试,三人的测试成绩如下表所示:| 测试项目 | 测试成绩/分 | ||
| 甲 | 乙 | 丙 | |
| 笔试 | 75 | 80 | 90 |
| 面试 | 93 | 70 | 68 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 植树棵数 | 3 | 4 | 5 | 6 |
| 人数 | 20 | 15 | 10 | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com