
如图,矩形ABCD中,AB=8,BC=10,点P在矩形的边DC上由D向C运动.沿直线AP翻折△ADP,形成如下四种情形.设DP=x,△ADP和矩形重叠部分(阴影)的面积为y.

(1)如图丁,当点P运动到与C重合时,求重叠部分的面积y;
(2)如图乙,当点P运动到何处时,翻折△ADP后,点D恰好落在BC边上?这时重叠部分的面积y等于多少?
(3)阅读材料:
已知锐角α≠45°,tan2α是角2α的正切值,它可以用角α的正切值tanα来表示,即![]() (α≠45°).
(α≠45°).
根据上述阅读材料,求出用x表示y的解析式,并指出x的取值范围.(提示:在图丙中可设∠DAP=α)
(1)由题意可得∠DAC=∠![]() AC=∠ACE,∴AE=CE.
AC=∠ACE,∴AE=CE.
设AE=CE=m,则BE=10-m.
在Rt△ABE中,得m2=82+(10-m)2,m=8.2.
∴重叠部分的面积y=![]() ·CE·AB=
·CE·AB=![]() ×8.2×8=32.8(平方单位).
×8.2×8=32.8(平方单位).
另法过E作EO⊥AC于O,由Rt△ABC∽Rt△EOC可求得EO.
(2)由题意可得△DAP≌△![]() AP,
AP,
∴A![]() =AD=10,P
=AD=10,P![]() =DP=x.
=DP=x.
在Rt△AB![]() 中,∵AB=8,∴B
中,∵AB=8,∴B![]() =
=![]() =6,于是C
=6,于是C![]() =4.
=4.
在Rt△PC![]() 中,由x2=42+(8-x)2,得x=5.
中,由x2=42+(8-x)2,得x=5.
此时y=![]() ·AD·DP=
·AD·DP=![]() ×10×5=25(平方单位).
×10×5=25(平方单位).
表明当DP=5时,点D恰好落在BC边上,这时y=25.
另法由Rt△AB![]() ∽Rt△PC
∽Rt△PC![]() 可求得DP.
可求得DP.
(3)由(2)知,DP=5是甲、丙两种情形的分界点.
当0≤x≤5时,由图甲知y=![]() =S△ADP=
=S△ADP=![]() ·AD·DP=5x.
·AD·DP=5x.
当5<x<8时,如图丙,设∠DAP=α,则∠AEB=2α,∠FPC=2α.
在Rt△ADP中,得tanα=![]() .
.
根据阅读材料,得tan2α=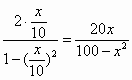 .
.
在Rt△ABE中,有BE=AB/tan2α=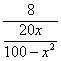 =
=![]() .
.
同理,在Rt△PCF中,有CF=(8-x)tan2α=![]() .
.
∴△ABE的面积
S△ABE=![]() ·AB·BE=
·AB·BE=![]() ×8×
×8×![]() =
=![]() .
.
△PCF的面积
S△PCF=![]() ·PC·CF=
·PC·CF=![]() (8-x)×
(8-x)×![]() =
=![]() .
.
而直角梯形ABCP的面积为
S梯形ABCP=![]() (PC+AB)×BC=
(PC+AB)×BC=![]() (8-x+8)×10=80-5x.
(8-x+8)×10=80-5x.
故重叠部分的面积y=S梯形ABCP-S△ABE-S△PCF=80-5x-![]() -
-![]() .
.
经验证,当x=8时,y=32.8适合上式.
综上所述,当0≤x≤5时,y=5x;当5<x≤8时,y=80-5x-![]() -
-![]() .
.


 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:初中数学 来源: 题型:
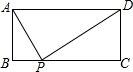 如图,矩形ABCD中,AD=a,AB=b,要使BC边上至少存在一点P,使△ABP、△APD、△CDP两两相似,则a、b间的关系式一定满足( )
如图,矩形ABCD中,AD=a,AB=b,要使BC边上至少存在一点P,使△ABP、△APD、△CDP两两相似,则a、b间的关系式一定满足( )A、a≥
| ||
| B、a≥b | ||
C、a≥
| ||
| D、a≥2b |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2008•怀柔区二模)已知如图,矩形ABCD中,AB=3cm,BC=4cm,E是边AD上一点,且BE=ED,P是对角线上任意一点,PF⊥BE,PG⊥AD,垂足分别为F、G.则PF+PG的长为
(2008•怀柔区二模)已知如图,矩形ABCD中,AB=3cm,BC=4cm,E是边AD上一点,且BE=ED,P是对角线上任意一点,PF⊥BE,PG⊥AD,垂足分别为F、G.则PF+PG的长为查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com