
【题目】如图,在△ABC中,∠ABC=90°,AC的垂直平分线分别与AC,BC及AB的延长线相交于点D,E,F,点O是EF中点,连结BO井延长到G,且GO=BO,连接EG,FG
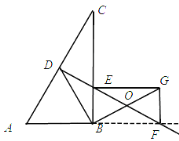
(1)试求四边形EBFG的形状,说明理由;
(2)求证:BD⊥BG
(3)当AB=BE=1时,求EF的长,
【答案】(1) 四边形EBFG是矩形;(2)证明见解析;(3)![]() .
.
【解析】
(1)根据对角线互相平分的四边形平行四边形可得四边形EBFG是平行四边形,再由∠CBF=90°,即可判断EBFG是矩形.
(2)由直角三角形斜边中线等于斜边一半可知BD=CD,OB=OE,即可得∠C=∠CBD,∠OEB=∠OBE,由∠FDC=90°即可得∠DBG=90°;
(3)连接AE,由AB=BE=1勾股定理易求AE=![]() ,结合已知易证△ABC≌△EBF,得BF=BC=1+
,结合已知易证△ABC≌△EBF,得BF=BC=1+![]() 再由勾股定理即可求出EF=
再由勾股定理即可求出EF=![]() .
.
解:(1)结论:四边形EBFG是矩形.
理由:∵OE=OF,OB=OG,
∴四边形EBFG是平行四边形,
∵∠ABC=90°即∠CBF=90°,
∴EBFG是矩形.
(2)∵CD=AD,∠ABC=90°,
∴BD=CD
∴∠C=∠CBD,
同理可得:∠OEB=∠OBE,
∵DF垂直平分AC,即∠EDC=90°,
∴∠C+∠DEC=90°,
∵∠DEC=∠OEB,
∴∠CBD+∠OBE=90°,
∴BD⊥BG.
(3)如图:连接AE,
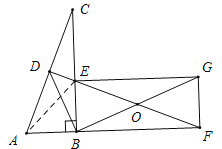
在Rt△ABE中,AB=BE=1,
∴AE=![]() ,
,
∵DF是AC垂直平分线,
∴AE=CE,
∴BC=1+![]()
∵∠CDE=∠CBF=90°,
∴∠C=∠BFE,
在△ABC和△EBF中,
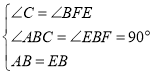 ,
,
∴△ABC≌△EBF(AAS)
∴BF=BC,
在Rt△BEF中,BE=1,BF=1+![]() ,
,
∴EF=![]()
![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,图象中所反映的过程是:张强从家跑步去体育场,在那里锻炼了一阵后,又 去早餐店吃早餐,然后散步走回家,其中 x 表示时间,y 表示张强离家的距离。根据图象提供的信息,以下四个说法错误的是( )

A. 体育场离张强家2.5千米 B. 张强在体育场锻炼了15分钟
C. 体育场离早餐店4千米 D. 张强从早餐店回家的平均速度是3千米/小时
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,O为坐标原点.
(1)已知点A(3,1),连接OA,作如下探究:
探究一:平移线段OA,使点O落在点B,设点A落在点C,若点B的坐标为(1,2),请在图①中作出BC,点C的坐标是__________.
探究二:将线段OA绕点O逆时针旋转90°,设点A落在点D,则点D的坐标是__________;连接AD,则AD=________(图②为备用图).
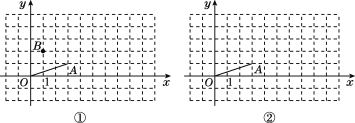
(2)已知四点O(0,0),A(a,b),C,B(c,d),顺次连接O,A,C,B,O,若所得到的四边形为平行四边形,则点C的坐标是____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在梯形ABCD中,∠BCD=∠D=90,上底AD=3,下底BC=![]() ,高CD=4,沿AC把梯形ABCD翻折,点D是恰好落在AB边上的点E处,求△BCE面积。
,高CD=4,沿AC把梯形ABCD翻折,点D是恰好落在AB边上的点E处,求△BCE面积。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是小江家的住房户型结构图.根据结构图提供的信息,解答下列问题:

(1)用含a、b的代数式表示小江家的住房总面积S;
(2)小江家准备给房间重新铺设地砖.若卧室所用的地砖价格为每平方米50元;卫生间、厨房和客厅所用的地砖价格为每平方米40元.请用含a、b的代数式表示铺设地砖的总费用W;
(3)在(2)的条件下,当a=6,b=4时,求W的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
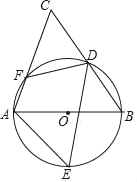
【题目】如图,AB是⊙O的直径,D、E为⊙O上位于AB异侧的两点,连接BD并延长至点C,使得CD=BD,连接AC交⊙O于点F,连接AE、DE、DF.
(1)求证:∠E=∠C;
(2)若DF=6cm,cosB=![]() ,E是弧AB的中点,求DE的长.
,E是弧AB的中点,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
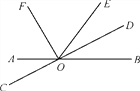
【题目】如图,直线AB与CD相交于点O,OF,OD分别是∠AOE,∠BOE的平分线.
(1)写出∠DOE的补角;
(2)若∠BOE=62°,求∠AOD和∠EOF的度数;
(3)试问射线OD与OF之间有什么特殊的位置关系?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A和点B在数轴上对应的数分别为a和b,且(a+6)2+|b﹣8|=0.
(1)求线段AB的长;
(2)点C在数轴上所对应的数为x,且x是方程x﹣1=![]() x+1的解,在线段AB上是否存在点D,使得AD+BD=
x+1的解,在线段AB上是否存在点D,使得AD+BD=![]() CD?若存在,请求出点D在数轴上所对应的数,若不存在,请说明理由;
CD?若存在,请求出点D在数轴上所对应的数,若不存在,请说明理由;
(3)在(2)的条件下,线段AD和BC分别以6个单位长度/秒和5个单位长度/秒的速度同时向右运动,运动时间为t秒,M为线段AD的中点,N为线段BC的中点,若MN=12,求t的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上有A,B,C三点,分别代表﹣30,﹣10,10,两只电子蚂蚁甲,乙分别从A,C两点同时相向而行,甲的速度为4个单位/秒,乙的速度为6个单位/秒.

(1)甲,乙经过多少秒在数轴上相遇,并求出相遇点表示的数?
(2)多少秒后,甲到A,B,C的距离和为48个单位?
(3)在甲到A、B、C的距离和为48个单位时,若甲调头并保持速度不变,则甲,乙还能在数轴上相遇吗?若能,求出相遇点;若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com