
【题目】 若一个三角形一条边的平方等于另两条边的乘积,我们把这个三角形叫做比例三角形.
(1)已知△ABC是比例三角形,AB=2,BC=3,请直接写出所有满足AC条件的长;
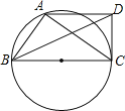
(2)如图,点A在以BC为直径的圆上,BD平分∠ABC,AD∥BC,∠ADC=90°.
①求证:△ABC为比例三角形;
②求![]() 的值.
的值.
(3)若以点C为顶点的抛物线y=mx2-4mx-12m(m<0)与x轴交于A、B两点,△ABC是比例三角形,若点M(x0,y0)为该抛物线上任意一点,总有n-![]() ≤-
≤-![]() my02-40
my02-40![]() y0+298成立,求实数n的最大值.
y0+298成立,求实数n的最大值.
【答案】(1)![]() ,
,![]() ,
,![]() ;(2)①证明见解析;②
;(2)①证明见解析;②![]() ;(3)10+
;(3)10+![]() .
.
【解析】
(1)先由三角形两边之和大于第三边、两边之差小于第三边,求出AC长度的范围.因为三角形三边都有可能是平方等于另两边乘积的边,故需分三种情况讨论,计算并判断结果是否合理.
(2)①由BD平分∠ABC和AD∥BC可证得∠ABD=∠DBC=∠ADB,进而得AB=AD.因为BC为圆的直径,根据圆周角定理得∠BAC=∠CDA=90°,再加上平行所得的∠ACB=∠DAC,即证得△ABC∽△DCA,由对应边成比例得AC2=BCDA=BCAB,得证.
②由Rt△ABC、Rt△ACD、Rt△BCD根据勾股定理得BD2=BC2+CD2=AB2+AC2+AC2-AB2=2AC2,故有BD=![]() AC,进而得
AC,进而得![]() .
.
(3)先由抛物线解析式求点A、B、C坐标,求得AB=8,根据抛物线对称性有AC=BC.由△ABC是比例三角形可得AB2=BCAC或AC2=ABBC,化简后都得到AC=AB,把含m的式子代入即求得m的值,进而求得抛物线解析式和最大值.由于点M(x0,y0)在抛物线上,则得到y0的最大值.设z=-![]() my02-40
my02-40![]() y0+298,把m的值代入并配方,得到关于y0的二次函数关系,且对应抛物线开口向下.由于y0范围取不到此二次函数的顶点,故取y0的最大值求得z的最小值,进而得到n的最大值.
y0+298,把m的值代入并配方,得到关于y0的二次函数关系,且对应抛物线开口向下.由于y0范围取不到此二次函数的顶点,故取y0的最大值求得z的最小值,进而得到n的最大值.
(1)∵AB=2,BC=3,
∴1<AC<5,
①若AB2=BCAC,则AC=![]() ,
,
②若BC2=ABAC,则AC=![]() ,
,
③若AC2=ABBC=6,则AC=![]() ,
,
综上所述,满足条件的AC的长为![]() ,
,![]() ,
,![]() .
.
(2)①证明:∵AD∥BC,
∴∠DAC=∠ACB,∠ADB=∠DBC,
∵BD平分∠ABC,
∴∠ABD=∠DBC,
∴∠ABD=∠ADB,
∴AB=AD,
∵点A在以BC为直径的圆上,
p>∴∠BAC=90°,∵∠BAC=∠CDA=90°,∠ACB=∠DAC,
∴△ABC∽△DCA,
∴![]() ,
,
∴AC2=BCDA=BCAB,
∴△ABC为比例三角形,
②∵∠BAC=∠CDA=90°,AB=AD,
∴BC2=AB2+AC2,AC2=AD2+CD2=AB2+CD2,
∵AD∥BC,
∴∠BCD=180°-∠ADC=90°,
∴BD2=BC2+CD2=AB2+AC2+AC2-AB2=2AC2,
∴BD=![]() AC,
AC,
∴![]() ;
;
(3)∵y=mx2-4mx-12m=m(x-2)2-16m(m<0),
∴抛物线开口向下,顶点C(2,-16m),
∵y=0时,mx2-4mx-12m=0,
解得:x1=-2,x2=6,
∴A(-2,0),B(6,0),AB=8,
∴AC=BC=![]() ,
,
∵△ABC是比例三角形,
∴AB2=BCAC或AC2=ABBC,
∴AB=AC,
∴4![]() =8,
=8,
解得:m1=![]() (舍去),m2=-
(舍去),m2=-![]() ,
,
∴抛物线解析式为y=-![]() x2+
x2+![]() x+3
x+3![]() =-
=-![]() (x-2)2+4
(x-2)2+4![]() ,
,
∵M(x0,y0)在抛物线上,
∴y0≤4![]() ,
,
设z=-![]() my02-40
my02-40![]() y0+298=4y02-40
y0+298=4y02-40![]() y0+298=4(y0-5
y0+298=4(y0-5![]() )2-2,
)2-2,
∴当y0≤4![]() 时,z随x的增大而减小,
时,z随x的增大而减小,
∴y0=4![]() 时,z最小值=4×(4
时,z最小值=4×(4![]() -5
-5![]() )2-2=4×3-2=10,
)2-2=4×3-2=10,
∵n-![]() ≤z恒成立,即n-
≤z恒成立,即n-![]() ≤10,
≤10,
∴n的最大值为10+![]() .
.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:初中数学 来源: 题型:
【题目】 为更新果树品种,某果园计划新购进A、B两个品种的果树苗栽植培育,若计划购进这两种果树苗共45棵,其中A种苗的单价为7元/棵,购买B种苗所需费用y(元)与购买数量x(棵)之间存在如图所示的函数关系.
(1)求y与x的函数关系式;
(2)若在购买计划中,B种苗的数量不超过35棵,但不少于A种苗的数量,请设计购买方案,使总费用最低,并求出最低费用.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某路段上有A,B两处相距近200m且未设红绿灯的斑马线.为使交通高峰期该路段车辆与行人的通行更有序,交通部门打算在汽车平均停留时间较长的一处斑马线上放置移动红绿灯.图1,图2分别是交通高峰期来往车辆在A,B斑马线前停留时间的抽样统计图.根据统计图解决下列问题:
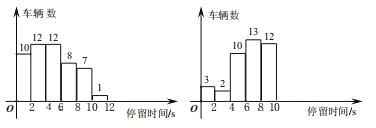
(1)若某日交通高峰期共有350辆车经过A斑马线,请估计该日停留时间为10s~12s的车辆数,以及这些停留时间为10s~12s的车辆的平均停留时间;(直接写出答案)
(2)移动红绿灯放置在哪一处斑马线上较为合适?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
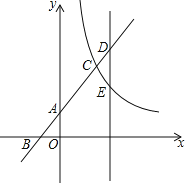
【题目】如图所示,直线y=x+2与坐标轴交于A、B两点,与反比例函数y=![]() (x>0)交于点C,已知AC=2AB.
(x>0)交于点C,已知AC=2AB.
(1)求反比例函数解析式;
(2)若在点C的右侧有一平行于y轴的直线,分别交一次函数图象与反比例函数图象于D、E两点,若CD=CE,求点D坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,将两块全等的直角三角形纸片△ABC和△DEF叠放在一起,其中∠ACB=∠E=90°,BC=DE=6,AC=FE=8,顶点D与边AB的中点重合.
(1)若DE经过点C,DF交AC于点G,求重叠部分(△DCG)的面积;
(2)合作交流:“希望”小组受问题(1)的启发,将△DEF绕点D旋转,使DE⊥AB交AC于点H,DF交AC于点G,如图2,求重叠部分(△DGH)的面积.
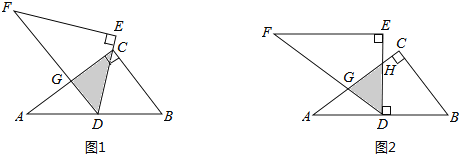
查看答案和解析>>
科目:初中数学 来源: 题型:
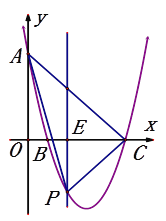
【题目】在平面直角坐标系中,抛物线![]() 与y轴的交点为A,与x轴的正半轴分别交于点B(b,0),C(c,0).
与y轴的交点为A,与x轴的正半轴分别交于点B(b,0),C(c,0).
(1)当b=1时,求抛物线相应的函数表达式;
(2)当b=1时,如图,E(t,0)是线段BC上的一动点,过点E作平行于y轴的直线l与抛物线的交点为P.求△APC面积的最大值;
(3)当c =b+ n.时,且n为正整数.线段BC(包括端点)上有且只有五个点的横坐标是整数,求b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:![]() 是
是![]() 的角平分线,点
的角平分线,点![]() ,
,![]() 分别在
分别在![]() ,
,![]() 上,且
上,且![]() ,
,![]()
(1)如图1,求证:四边形![]() 是平行四边形;
是平行四边形;
(2)如图2,若![]() 为等边三角形,在不添加辅助线的情况下,请你直接写出所有的全等三角形.
为等边三角形,在不添加辅助线的情况下,请你直接写出所有的全等三角形.
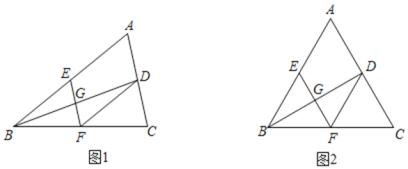
查看答案和解析>>
科目:初中数学 来源: 题型:
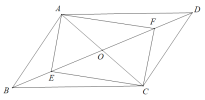
【题目】如图,平行四边形ABCD中,AC、BD相交于点O,E、F是对角线BD上的点,且BE=DF,连接AE、CE、CF、AF.
(1)求证:AE=CF;
(2)若平行四边形ABCD的面积是12,△OCF的面积是2,求△ADF的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com