
【题目】如图,在△ABC中,∠ACB=90°,∠B=30°,CD,CE分别是AB边上的中线和高.

(1)求证:AE=ED;
(2)若AC=2,求△CDE的周长.
【答案】(1)见解析(2)![]()
【解析】
试题分析:(1)根据直角三角形斜边上的中线等于斜边的一半,得CD=AD,根据直角三角形的两个锐角互余,得∠A=60°,从而判定△ACD是等边三角形,再根据等腰三角形的三线合一的性质即可证明;
(2)结合(1)中的结论,求得CD=2,DE=1,只需根据勾股定理求得CE的长即可.
(1)证明:∵∠ACB=90°,CD是AB边上的中线,
∴CD=AD=DB.
∵∠B=30°,
∴∠A=60°.
∴△ACD是等边三角形.
∵CE是斜边AB上的高,
∴AE=ED.
(2)解:由(1)得AC=CD=AD=2ED,
又AC=2,
∴CD=2,ED=1.
∴![]() .
.
∴△CDE的周长=![]() .
.


 计算高手系列答案
计算高手系列答案科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b(k≠0)的图象过点P(﹣![]() ,0),且与反比例函数y=
,0),且与反比例函数y=![]() (m≠0)的图象相交于点A(﹣2,1)和点B.
(m≠0)的图象相交于点A(﹣2,1)和点B.
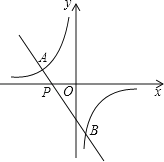
(1)求一次函数和反比例函数的解析式;
(2)求点B的坐标,并根据图象回答:当x在什么范围内取值时,一次函数的函数值小于反比例函数的函数值?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2015年4月,生物学家发现一种病毒的长度约为0.0000043米,利用科学记数法表示为( )
A. 4.3×106米 B. 4.3×10﹣5米 C. 4.3×10﹣6米 D. 43×107米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某兴趣小组有7名成员,他们的年龄(单位:岁)分别为:13,14,14,15,13,14,15,则他们年龄的众数和中位数分别为( )
A.13,14
B.14,14
C.14,13.5
D.14,13
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列结论正确的是( )
A. 两直线被第三条直线所截,同位角相等
B. 三角形的一个外角等于两个内角的和
C. 多边形最多有三个外角是钝角
D. 连接平面上三点构成的图形是三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正比例函数![]() 的图象与反比例函数
的图象与反比例函数![]() (
(![]() 为常数,
为常数,![]() )的图象有一个交点的横坐标是2.
)的图象有一个交点的横坐标是2.
(1)求两个函数图象的交点坐标;
(2)若点![]() ,
,![]() 是反比例函数
是反比例函数![]() 图象上的两点,且
图象上的两点,且![]() ,试比较
,试比较![]() 的大小.
的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com