
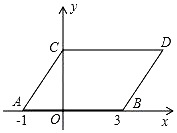
 如图,在平面直角坐标系中,点A,B的坐标分别为(-1,0),(3,0),现同时将点A,B分别向上平移2个单位,再向右平移1个单位,分别得到点A,B的对应点C,D,连接AC,BD,CD.得平行四边形ABDC
如图,在平面直角坐标系中,点A,B的坐标分别为(-1,0),(3,0),现同时将点A,B分别向上平移2个单位,再向右平移1个单位,分别得到点A,B的对应点C,D,连接AC,BD,CD.得平行四边形ABDC分析 (1)根据向上平移纵坐标加,向右平移横坐标加求出点C、D的坐标即可,
(2)利用平行四边形的面积公式和三角形的面积公式列式计算即可得;
(3)分三种情况,根据平移的性质可得AB∥CD,再过点P作PE∥AB,根据平行公理可得PE∥CD,然后根据两直线平行,内错角相等可得∠DCP=∠CPE,∠BOP=∠OPE即可得出结论.
解答 解:(1)∵将A(-1,0),B(3,0)分别向上平移2个单位,再向右平移1个单位,
∴C(0,2),D(4,2);
(2)∵AB=4,CO=2,
∴S平行四边形ABDC=AB•CO=4×2=8,
设M坐标为(0,m),
∴$\frac{1}{2}$×4×|m|=8,解得m=±4
∴M点的坐标为(0,4)或(0,-4);
(3)①当点P在BD上,如图1,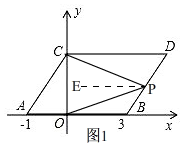
由平移的性质得,AB∥CD,
过点P作PE∥AB,则PE∥CD,
∴∠DCP=∠CPE,∠BOP=∠OPE,
∴∠CPO=∠CPE+∠OPE=∠DCP+∠BOP,
②当点P在线段BD的延长线上时,如图2,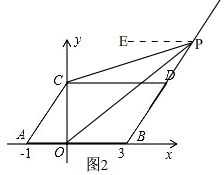
由平移的性质得,AB∥CD,
过点P作PE∥AB,则PE∥CD,
∴∠DCP=∠CPE,∠BOP=∠OPE,
∴∠CPO=∠OPE-∠CPE=∠BOP-∠DCP,
③当点P在线段DB的延长线上时,如图3,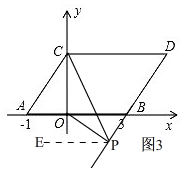 同(2)的方法得出∠CPO=∠DCP-∠BOP.
同(2)的方法得出∠CPO=∠DCP-∠BOP.
点评 此题是四边形综合题,主要考查了平移的平移的性质,平行线的性质,三角形的面积公式,平行四边形的面积计算方法,解本题的关键是作出图形,是一道比较简单的中考常考题.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:初中数学 来源: 题型:解答题
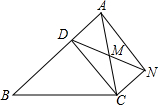 已知:如图,D是△ABC的边AB上一点,CN∥AB,DN交AC于点M,MA=MC.
已知:如图,D是△ABC的边AB上一点,CN∥AB,DN交AC于点M,MA=MC.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
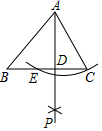 如图,已知锐角三角形ABC,以点A为圆心,AC为半径画弧与BC交于点E,分别以点E、C为圆心,以大于$\frac{1}{2}$EC的长为半径画弧相交于点P,作射线AP,交BC于点D.若BC=5,AD=4,tan∠BAD=$\frac{3}{4}$,则AC的长为( )
如图,已知锐角三角形ABC,以点A为圆心,AC为半径画弧与BC交于点E,分别以点E、C为圆心,以大于$\frac{1}{2}$EC的长为半径画弧相交于点P,作射线AP,交BC于点D.若BC=5,AD=4,tan∠BAD=$\frac{3}{4}$,则AC的长为( )| A. | 3 | B. | 5 | C. | $\sqrt{5}$ | D. | 2$\sqrt{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 年级 | 筹集资金数额 | 资助贫困中学 | 资助贫困小学生人数(名) |
| 七年级 | 5000 | 2 | 5 |
| 八年级 | 6000 | 3 | 5 |
| 九年级 | 8000 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com