
【题目】如图,已知BE,CF分别是△ABC中AC,AB边上的高线,在BE的延长线上取点P,使PB=AC,在CF的延长线上取点Q,使CQ=AB.求证:AQ⊥AP.

科目:初中数学 来源: 题型:
【题目】如图,在方格纸内将△ABC水平向右平移4个单位得到△A′B′C′.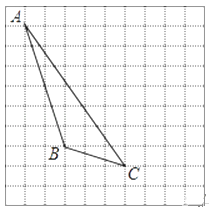
(1)补全△A′B′C′,利用网格点和直尺画图
(2)图中AC与A1C1的关系是:
(3)画出AB边上的高线CD;
(4)画出△ABC中AB边上的中线CE
(5)△BCE的面积为
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c与x轴相交于A(﹣2,0),B(4,0),与y轴相交于点C,且抛物线经过点(2,2).
(1)求此抛物线的解析式;
(2)在抛物线的对称轴上找一点H,使AH+CH最小,并求出点H的坐标;
(3)在第四象限内,抛物线上是否存在点M,是的以点A、B、M为顶点的三角形与△ABC相似?若存在,请求出点M的坐标;若不存在,请说明理由.
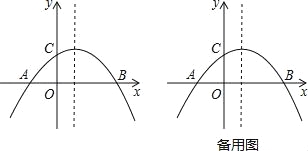
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)![]()
(2)20132﹣2012×2014(简便计算)
(3)(3a2)3+a2a4﹣a8÷a2
(4)(x﹣2)(3x﹣1)
(5)(x﹣1)(x+1)﹣(x+2)2
(6)(a+3b﹣2c)(a﹣3b﹣2c)
(7)(m﹣2n+1)2
(8)(2a﹣3b)2(2a+3b)2 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们运用图(Ⅰ)中大正方形的面积可表示为(a+b)2 , 也可表示为c3+4(![]() ab),即(a+b)2=c2+4(
ab),即(a+b)2=c2+4(![]() ab)由此推导出一个重要的结论a2+b2=c2 , 这个重要的结论就是著名的“勾股定理”.这种根据图形可以极简单地直观推论或验证数学规律和公式的方法,简称“无字证明”.
ab)由此推导出一个重要的结论a2+b2=c2 , 这个重要的结论就是著名的“勾股定理”.这种根据图形可以极简单地直观推论或验证数学规律和公式的方法,简称“无字证明”.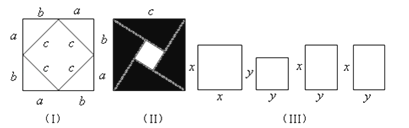
(1)请你用图(Ⅱ)(2002年国际数学家大会会标)的面积表达式验证勾股定理(其中四个直角三角形的较大的直角边长都为a,较小的直角边长都为b,斜边长都为c).
(2)请你用(Ⅲ)提供的图形进行组合,用组合图形的面积表达式验证:(x+2y)2=x2+4xy+4y2 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,图①是一块边长为1,周长记为P1的等边三角形纸板,沿图①的底边剪去一块边长的![]() 的等边三角形纸板后得到图②,然后沿同一底边依次剪去一块更小的等边三角形纸板(即其边长为前一块被剪掉等边三角形纸板边长的
的等边三角形纸板后得到图②,然后沿同一底边依次剪去一块更小的等边三角形纸板(即其边长为前一块被剪掉等边三角形纸板边长的![]() )后,得图③,④,…,记第n(n≥3)块纸板的周长为Pn,则Pn-Pn-1=_________
)后,得图③,④,…,记第n(n≥3)块纸板的周长为Pn,则Pn-Pn-1=_________
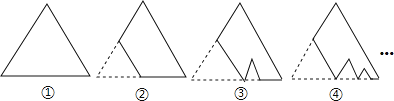
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,真命题是( )
A. 一组对边平行,另一组对边相等的四边形一定是等腰梯形
B. 对角线互相垂直的四边形是菱形
C. 顺次连结菱形各边中点所得的四边形是正方形
D. 四个内角均相等的四边形是矩形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表为宁波市2016年4月上旬10天的日最低气温情况,则这10天中日最低气温的中位数和众数分别是( )
温度(℃) | 11 | 13 | 14 | 15 | 16 |
天数 | 1 | 5 | 2 | 1 | 1 |
A.14℃,14℃
B.14℃,13℃
C.13℃,13℃
D.13℃,14℃
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com