
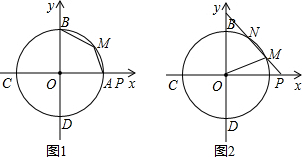
分析 (1)连接OM,过点M作MH⊥x轴于H,如图1,只需运用勾股定理就可求出圆的半径,只需利用弧的度数与所对圆心角的度数及所对圆周角的度数,就可求出∠AMB;
(2)①过点M作MH⊥x轴于H,如图2,只需用k的代数式表示OP即可,只需求出直线PM与x轴的交点即可,由条件“直线y=kx+b与⊙O的另一个交点N在弧BM上(不和点B、M重合)”可得到k的范围,从而可求出S的范围;②连接ON交BM于E,过点E作EF⊥y轴于F,过点N作NG⊥y轴于G,如图3,运用中点坐标公式可求出点E的坐标,易证△OEF∽△ONG,根据相似三角形的性质可求出点N的坐标,就可求出直线PM的关系式;
(3)当点P与点A重合时,可求出此时k=-3,易知当∠ACQ=90°及∠AQC=90°时,满足要求的点Q各1个,共2个;当点P与点A不重合时,此时k≠-3,易知当∠ACQ=90°及∠CAQ=90°时,满足要求的点Q各1个,当∠AQC=90°时,点Q在⊙O上,当PM与⊙O相切时,⊙O与直线PM只有1个交点,此时点Q与点M重合,易求出此时点P的坐标,即可得到k=-$\frac{4}{3}$,当PM与⊙O不相切时,⊙O与直线PM有2个交点,故点Q有2个,此时k<0,且k≠-$\frac{4}{3}$.问题得以解决.
解答 解:(1)连接OM,过点M作MH⊥x轴于H,如图1,
则有OH=4,MH=3M
∴OM=$\sqrt{{4}^{2}+{3}^{2}}$=5,
∴圆的半径为5.
∵∠AOB=90°,∴$\widehat{AB}$的度数为90°,
∴$\widehat{ACB}$的度数为270°,
∴∠AMB=135°.
故答案分别为5,135°;
(2)①过点M作MH⊥x轴于H,如图2,
则有MH=3.
∵点M(4,3)在直线y=kx+b上,
∴3=4k+b,
∴b=3-4k,
∴y=kx+3-4k.
当y=0时,0=kx+3-4k,
∴x=$\frac{4k-3}{k}$,
∴OP=$\frac{4k-3}{k}$,
∴S=$\frac{1}{2}$OP•MH=$\frac{1}{2}$•$\frac{4k-3}{k}$•3=6-$\frac{9}{2k}$.
∵直线y=kx+b与⊙O的另一个交点N在弧BM上(不和点B、M重合),
∴$\left\{\begin{array}{l}{k<0}\\{3-4k>5}\end{array}\right.$
解得k<-$\frac{1}{2}$,
∴-2k>1,
∴0<-$\frac{1}{2k}$<1,
∴0<-$\frac{9}{2k}$<9,
∴6<6-$\frac{9}{2k}$<15,
∴6<S<15;
②连接ON交BM于E,过点E作EF⊥y轴于F,过点N作NG⊥y轴于G,如图3,
则有EF∥NG,∠BON=∠MON.
∵OB=OM,∴BE=EM.
∵B(0,5),M(4,3),
∴E($\frac{0+4}{2}$,$\frac{5+3}{2}$)即(2,4),
∴EF=2,OF=4,
∴OE=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$.
∵EF∥NG,
∴△OEF∽△ONG,
∴$\frac{EF}{NG}$=$\frac{OF}{OG}$=$\frac{OE}{ON}$,
∴$\frac{2}{NG}$=$\frac{4}{OG}$=$\frac{2\sqrt{5}}{5}$,
∴NG=$\sqrt{5}$,OG=2$\sqrt{5}$,
∴点N的坐标为($\sqrt{5}$,2$\sqrt{5}$).
∵点E在直线y=kx+3-4k上,
∴2$\sqrt{5}$=$\sqrt{5}$k+3-4k,
解得k=$\frac{2-5\sqrt{5}}{11}$,
∴直线PM的函数关系式为y=$\frac{2-5\sqrt{5}}{11}$x+$\frac{25+20\sqrt{5}}{11}$;
(3)①当点P与点A重合时,P的坐标为(5,0),
则有0=5k+3-4k,解得k=-3.
Ⅰ.若∠ACQ=90°,则过点C垂直于AC的直线与PM的交点就是点Q,有1个;
Ⅱ.若∠CAQ=90°,则过点A垂直于AC的直线与PM的交点就是点Q,与点A重合,不存在;
Ⅲ.若∠AQC=90°,则点Q在⊙O上,此时点Q与点M重合(与点A重合时,△ACQ不存在),有1个;
∴当k=-3时,满足△ACQ为直角三角形的点Q有2个;
②当点P与点A不重合时,则有k≠-3.
Ⅰ.若∠ACQ=90°,则过点C垂直于AC的直线与PM的交点就是点Q,有1个;
Ⅱ.若∠CAQ=90°,则过点A垂直于AC的直线与PM的交点就是点Q,有1个;
Ⅲ.若∠AQC=90°,则点Q在⊙O上,
(a)当PM与⊙O相切时,⊙O与直线PM只有1个交点,此时点Q与点M重合,∠OMP=90°.
∵∠MOH=∠POM,∠OHM=∠OMP=90°,∴△OHM∽△OMP,
∴$\frac{OM}{OP}$=$\frac{OH}{OM}$,∴$\frac{5}{OP}$=$\frac{4}{5}$,∴OP=$\frac{25}{4}$,即P($\frac{25}{4}$,0),
∴0=$\frac{25}{4}$k+3-4k,解得k=-$\frac{4}{3}$.
(b)当PM与⊙O不相切时,⊙O与直线PM有2个交点,故点Q有2个,此时k<0,且k≠-$\frac{4}{3}$.
综上所述:当k=-3时,满足△ACQ为直角三角形的点Q有2个,
当k=-$\frac{4}{3}$时,满足△ACQ为直角三角形的点Q有3个,
当k<0,且k≠-$\frac{4}{3}$,k≠-3时,满足△ACQ为直角三角形的点Q有4个.
点评 本题主要考查了圆周角定理、直线与圆的位置关系、圆的切线的性质、直线与x轴的交点、解不等式组、相似三角形的判定与性质,中点坐标公式、等腰三角形的性质、勾股定理等知识,求出点E的坐标,进而求出点N的坐标是解决第(2)②小题的关键,正确进行分类是解决(3)小题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
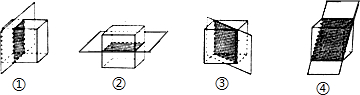
| A. | ①②相同‘③④相同 | B. | ①③相同;②④相同 | C. | ①④相同;②③相同 | D. | 都不相同 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com