
分析 (1)设打开甲的3把钥匙用A、A、A表示,打开乙的3把钥匙用B、B、B表示,再画树状展示所有30种等可能的结果数,接着找出恰好能打开两把锁的结果数,然后根据概率公式计算;
(2)想打开甲、乙两把锁,要由A、B,所以至少取2把,由于A或B只有3个,所以取4把时,一定含A和B.
解答 解:(1)设打开甲的3把钥匙用A、A、A表示,打开乙的3把钥匙用B、B、B表示,
画树状图为: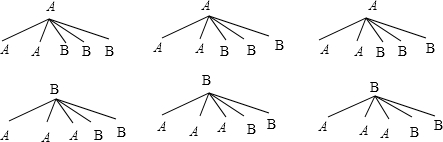
共有30种等可能的结果数,其中恰好能打开两把锁的结果数为18,
所以恰好能打开两把锁的概率=$\frac{18}{30}$=$\frac{3}{5}$;
(2)想打开甲、乙两把锁,至少取2把,至多取4把.
点评 本题考查了列表法与树状图法:利用列表法和树状图法展示所有可能的结果求出n,再从中选出符合事件A或B的结果数目m,求出概率.


科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{7}$ | C. | -2$\sqrt{7}$ | D. | 7$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
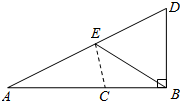 数学课上,老师按下面的方法作线段AB的黄金分割点C(如图),
数学课上,老师按下面的方法作线段AB的黄金分割点C(如图),查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增减 | +5 | -2 | 4 | +13 | 10 | +16 | 9 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
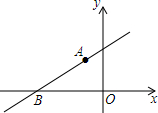 如图,直线y=kx+b经过A(-1,1)和B(-$\sqrt{7}$,0)两点,则不等式0<kx+b<-x的解集为-$\sqrt{7}$<x<-1.
如图,直线y=kx+b经过A(-1,1)和B(-$\sqrt{7}$,0)两点,则不等式0<kx+b<-x的解集为-$\sqrt{7}$<x<-1.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
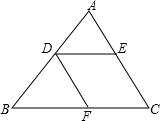 如图,DF∥AC,DE∥BC,下列各式中正确的是( )
如图,DF∥AC,DE∥BC,下列各式中正确的是( )| A. | $\frac{AD}{BD}$=$\frac{BF}{CF}$ | B. | $\frac{AE}{DE}$=$\frac{CE}{BC}$ | C. | $\frac{AE}{CE}$=$\frac{BD}{CD}$ | D. | $\frac{AD}{DE}$=$\frac{AB}{BC}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
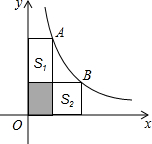 如图,A、B两点在双曲线y=$\frac{5}{2x}$(x>0)上,分别经过A、B两点向坐标轴作垂线段,已知S阴影=1,则S1+S2=3.
如图,A、B两点在双曲线y=$\frac{5}{2x}$(x>0)上,分别经过A、B两点向坐标轴作垂线段,已知S阴影=1,则S1+S2=3.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com