
【题目】已知二次函数 ![]() 的图像经过点
的图像经过点 ![]() .
.
(1)求这个二次函数的函数解析式;
(2)若抛物线交x轴于A,B两点,交y轴于C点,顶点为D,求以A、B、C、D为顶点的四边形面积.
【答案】
(1)解:将 (2,![]() ) 代入 y=x2+bx
) 代入 y=x2+bx![]() ,得:
,得:
4+2b![]() =
=![]() ,
,
∴ b=1 ,
∴二次函数解析式为 y=x2x![]() .
.
(2)解:∵抛物线交x轴于A,B两点,
∴A(![]() ,0),B(
,0),B(![]() ,0),
,0),
又∵抛物线交交y轴于C点,
∴C(0,![]() ),
),
又∵抛物线顶点为D,
∴D(![]() ,1) .
,1) .
∴S四边形ABCD= ![]() ×
×![]() ×
×![]() +
+![]() ×(
×(![]() +1)×
+1)×![]() +
+![]() ×1×1=
×1×1=![]() .
.
【解析】(1)将(2,![]() )代入函数解析式求出b的值,从而得出函数解析式.
)代入函数解析式求出b的值,从而得出函数解析式.
(2)根据题意分别求出A、B、C、D点的坐标,用分割法求出四边形ABCD的面积.
【考点精析】解答此题的关键在于理解抛物线与坐标轴的交点的相关知识,掌握一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.


 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:
【题目】如图,∠AOB=120°,OP平分∠AOB,且OP=2.若点M,N分别在OA,OB上,且△PMN为等边三角形,则满足上述条件的△PMN有( )

A. 2个 B. 3个 C. 4个 D. 无数个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知OM,ON分别是∠BOC和∠AOC的角平分线,∠AOB=86°,(1)∠MON=______(度);(2)当OC在∠AOB内绕点O转动时,∠MON的值______改变(填“会”或“不会”).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一段抛物线y=﹣x(x﹣3)(0≤x≤3),记为C1 , 它与x轴交于点O,A1;将C1绕点A1旋转180°得C2 , 交x 轴于点A2;将C2绕点A2旋转180°得C3 , 交x 轴于点A3;…如此进行下去,得到一条“波浪线”.若点P(37,m)在此“波浪线”上,则m的值为 . 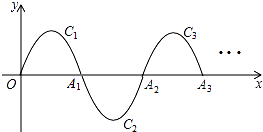
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,已知点A(﹣3,0)、B(0,4),对△OAB连续作旋转变换,依次得到△1、△2、△3、△4、…,△16的直角顶点的坐标为( )
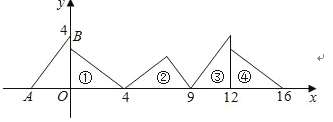
![]()
A. (60,0) B. (72,0) C. (67![]() ,
,![]() ) D. (79
) D. (79![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一张长方形的纸对折(使宽边重合,然后再对折),第一次对折,得到一条折痕连同长方形的两条宽边共3条等宽线(如图(1),第二次对折(每次的折痕与上次的折痕保持平行),得到5条等宽线(如图(2)所示),连续对折三次后,可以得到9条等宽线(如图(3所示),对折四次可以得到17条等宽线,如果对折6次,那么可以得到的等宽线条数是______条.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市实行阶梯电价制度,居民家庭每月用电量不超过80千瓦时时,实行“基本电价”;当每月用电量超过80千瓦时时,超过部分实行“提高电价”.去年小张家4月用电量为100千瓦时,交电费68元;5月用电量为120千瓦时,交电费88元.则基本电价”是__元/千瓦时,“提高电价”是__元/千瓦时.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系xOy中的点P和⊙C,给出如下定义:若存在过点P的直线l交⊙C于异于点P的A,B两点,在P,A,B三点中,位于中间的点恰为以另外两点为端点的线段的中点时,则称点P为⊙C 的相邻点,直线l为⊙C关于点P的相邻线.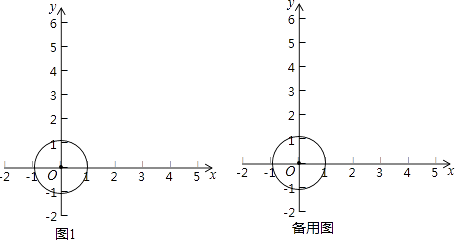
(1)当⊙O的半径为1时,
①分别判断在点D( ![]() ,
, ![]() ),E(0,﹣
),E(0,﹣ ![]() ),F(4,0)中,是⊙O的相邻点有;
),F(4,0)中,是⊙O的相邻点有;
②请从①中的答案中,任选一个相邻点,在图1中做出⊙O关于它的一条相邻线,并说明你的作图过程;
③点P在直线y=﹣x+3上,若点P为⊙O的相邻点,求点P横坐标的取值范围;
(2)⊙C的圆心在x轴上,半径为1,直线y=﹣ ![]() 与x轴,y轴分别交于点M,N,若线段MN上存在⊙C的相邻点P,直接写出圆心C的横坐标的取值范围.
与x轴,y轴分别交于点M,N,若线段MN上存在⊙C的相邻点P,直接写出圆心C的横坐标的取值范围.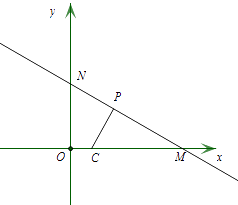
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校的某社团组织了一次智力竞赛,共a、b、c三题,每题或者得满分或者得0分,其中题a满分10分,题b、题c满分均为15分.竞赛结果,每个学生至少答对了一题,三题全答对的有2人,答对其中两道题的有14人,答对题a的人数与答对题b的人数之和为29,答对题a的人数与答对题c的人数之和为27,答对题b的人数与答对题c的人数之和为20,则这个社团的平均成绩是_____分.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com