
| 3 |
| 3 |

| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| BE |
| OE |
3
| ||
| 3 |
| 3 |
| DF |
| AF |
| ||
| 2-1 |
| 3 |
32+(3
|
(2-1)2+(
|
| AP |
| OA |
| AD |
| OB |
| AP |
| 2 |
| 2 |
| 6 |
| 2 |
| 3 |
| 2 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| AP |
| OB |
| AD |
| OA |
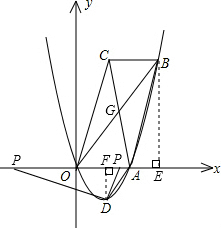
| AP |
| 6 |
| 2 |
| 2 |
| 4 |
| 3 |
|
|
| ||
| 3 |
2
| ||
| 3 |
2
| ||
| 3 |
2
| ||
| 3 |


 АйФъбЇЕфПЮЪБбЇСЗВтЯЕСаД№АИ
АйФъбЇЕфПЮЪБбЇСЗВтЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃКВЛЯъ ЬтаЭЃКНтД№Ьт
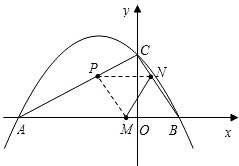 BCЃЌBЁЂCСНЕуЕФзјБъЗжБ№ЮЊBЃЈ1ЃЌ0ЃЉЁЂC(0ЃЌ
BCЃЌBЁЂCСНЕуЕФзјБъЗжБ№ЮЊBЃЈ1ЃЌ0ЃЉЁЂC(0ЃЌ| 3 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃКВЛЯъ ЬтаЭЃКНтД№Ьт
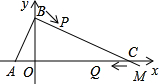 ЁЂQЁЂCЮЊЖЅЕуЕФШ§НЧаЮЪЧЕШбќШ§НЧаЮЃЎЃЈЕуPЕНЕуCЪБЭЃжЙдЫЖЏЃЌЕуQвВЭЌЪБЭЃжЙдЫЖЏЃЉЃЌЧѓtЕФжЕЃЎ
ЁЂQЁЂCЮЊЖЅЕуЕФШ§НЧаЮЪЧЕШбќШ§НЧаЮЃЎЃЈЕуPЕНЕуCЪБЭЃжЙдЫЖЏЃЌЕуQвВЭЌЪБЭЃжЙдЫЖЏЃЉЃЌЧѓtЕФжЕЃЎВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃКВЛЯъ ЬтаЭЃКНтД№Ьт
| 1 |
| 4 |
| 1 |
| 2 |

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃКВЛЯъ ЬтаЭЃКНтД№Ьт

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃКВЛЯъ ЬтаЭЃКЬюПеЬт
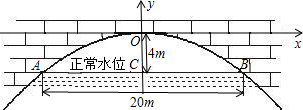
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃКВЛЯъ ЬтаЭЃКНтД№Ьт
| 15 |
| 2 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃКВЛЯъ ЬтаЭЃКЕЅбЁЬт
| AЃЎ2009 | BЃЎ2012 | CЃЎ2011 | DЃЎ2010 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃКВЛЯъ ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com