
ЁОЬтФПЁПЖЈвхЃКШєХзЮяЯпЕФЖЅЕугыxжсЕФСНИіНЛЕуЙЙГЩЕФШ§НЧаЮЪЧжБНЧШ§НЧаЮЃЌдђетжжХзЮяЯпБЛГЦЮЊЃКЁАжБНЧХзЮяЯпЁБЃЎШчЭМЃЌжБЯпlЃКyЃН![]() x+bОЙ§ЕуM(0ЃЌ
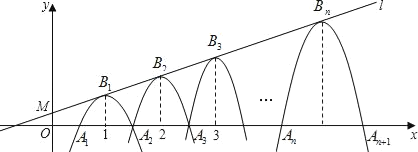
x+bОЙ§ЕуM(0ЃЌ![]() )ЃЌвЛзщХзЮяЯпЕФЖЅЕуB1(1ЃЌy1)ЃЌB2(2ЃЌy2)ЃЌB3(3ЃЌy3)ЃЌЁBn(nЃЌyn)ЁЁ(nЮЊе§ећЪ§)ЃЌвРДЮЪЧжБЯпlЩЯЕФЕуЃЌЕквЛИіХзЮяЯпгыxжсе§АыжсЕФНЛЕуA1(x1ЃЌ0)КЭA2(x2ЃЌ0)ЃЌЕкЖўИіХзЮяЯпгыxжсНЛЕуA2(x2ЃЌ0)КЭA3(x3ЃЌ0)ЃЌвдДЫРрЭЦЃЌШєx1ЃНd(0ЃМdЃМ1)ЃЌЕБdЮЊ_____ЪБЃЌетзщХзЮяЯпжаДцдкжБНЧХзЮяЯпЃЎ
)ЃЌвЛзщХзЮяЯпЕФЖЅЕуB1(1ЃЌy1)ЃЌB2(2ЃЌy2)ЃЌB3(3ЃЌy3)ЃЌЁBn(nЃЌyn)ЁЁ(nЮЊе§ећЪ§)ЃЌвРДЮЪЧжБЯпlЩЯЕФЕуЃЌЕквЛИіХзЮяЯпгыxжсе§АыжсЕФНЛЕуA1(x1ЃЌ0)КЭA2(x2ЃЌ0)ЃЌЕкЖўИіХзЮяЯпгыxжсНЛЕуA2(x2ЃЌ0)КЭA3(x3ЃЌ0)ЃЌвдДЫРрЭЦЃЌШєx1ЃНd(0ЃМdЃМ1)ЃЌЕБdЮЊ_____ЪБЃЌетзщХзЮяЯпжаДцдкжБНЧХзЮяЯпЃЎ
ЁОД№АИЁП![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]()
ЁОНтЮіЁП
гЩХзЮяЯпЕФЖдГЦадПЩжЊЃЌЫљЙЙГЩЕФжБНЧШ§НЧаЮБиЪЧвдХзЮяЯпЖЅЕуЮЊжБНЧЖЅЕуЕФЕШбќШ§НЧаЮЃЌЫљвдДЫЕШбќШ§НЧаЮаББпЩЯЕФИпЕШгкаББпЕФвЛАыЃЎгж0ЃМdЃМ1ЃЌЫљвдЕШбќжБНЧШ§НЧаЮаББпЕФГЄаЁгк2ЃЌЫљвдЕШбќжБНЧШ§НЧаЮаББпЕФИпвЛЖЈаЁгк1ЃЌМДХзЮяЯпЕФЖЈЕузнзјБъБиЖЈаЁгк1ЃЎ
жБЯпlЃКyЃН![]() x+bОЙ§ЕуM(0ЃЌ
x+bОЙ§ЕуM(0ЃЌ![]() )ЃЌдђbЃН
)ЃЌдђbЃН![]() ЃЛ
ЃЛ
ЁржБЯпlЃКyЃН![]() ЃЎ
ЃЎ
гЩХзЮяЯпЕФЖдГЦаджЊЃКХзЮяЯпЕФЖЅЕугыxжсЕФСНИіНЛЕуЙЙГЩЕФжБНЧШ§НЧаЮБиЮЊЕШбќжБНЧШ§НЧаЮЃЛ
ЁрИУЕШбќШ§НЧаЮЕФИпЕШгкаББпЕФвЛАыЃЎ
Ёп0ЃМdЃМ1ЃЌ
ЁрИУЕШбќжБНЧШ§НЧаЮЕФаББпГЄаЁгк2ЃЌаББпЩЯЕФИпаЁгк1(МДХзЮяЯпЕФЖЅЕузнзјБъаЁгк1)ЃЛ
ЕБxЃН1ЪБЃЌ![]() ЃЌ
ЃЌ
ЕБxЃН2ЪБЃЌ![]() ЃЌ
ЃЌ
ЕБxЃН3ЪБЃЌ![]() ЃЌ
ЃЌ
ЕБxЃН4ЪБЃЌ![]() ЃЌ
ЃЌ
ЁржБНЧХзЮяЯпЕФЖЅЕужЛгаB1ЁЂB2ЁЎB3ЃЎ
ЂйШєB1ЮЊЖЅЕуЃЌгЩ![]() ЃЌдђ
ЃЌдђ![]() ЃЛ
ЃЛ
ЂкШєB2ЮЊЖЅЕуЃЌгЩ![]() ЃЌдђ
ЃЌдђ![]() ЃЛ
ЃЛ
ЂлШєB3ЮЊЖЅЕуЃЌгЩ![]() ЃЌдђdЃН
ЃЌдђdЃН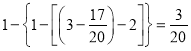 ЃЛ
ЃЛ
злЩЯЫљЪіЃЌdЕФжЕЮЊ![]() Лђ
Лђ![]() Лђ
Лђ![]() ЪБЃЎетзщХзЮяЯпжаДцдкжБНЧХзЮяЯпЃЎ
ЪБЃЎетзщХзЮяЯпжаДцдкжБНЧХзЮяЯпЃЎ
ЙЪД№АИЮЊЃК![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЃЎ
ЃЎ


 ПьНнгЂгяжмжмСЗЯЕСаД№АИ
ПьНнгЂгяжмжмСЗЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкМзЁЂввСНИіВЛЭИУїЕФВМДќЃЌМзДќжазАга3ИіЭъШЋЯрЭЌЕФаЁЧђЃЌЗжБ№БъгаЪ§зж0ЃЌ1ЃЌ2ЃЛввДќжазАга3ИіЭъШЋЯрЭЌЕФаЁЧђЃЌЗжБ№БъгаЪ§зжЉ1ЃЌЉ2ЃЌ0ЃЛЯжДгМзДќжаЫцЛњГщШЁвЛИіаЁЧђЃЌМЧТМБъгаЕФЪ§зжЮЊxЃЌдйДгввДќжаЫцЛњГщШЁвЛИіаЁЧђЃЌМЧТМБъгаЕФЪ§зжЮЊyЃЌШЗЖЈЕуMзјБъЮЊЃЈxЃЌyЃЉЃЎ
ЃЈ1ЃЉгУЪїзДЭМЛђСаБэЗЈСаОйЕуMЫљгаПЩФмЕФзјБъЃЛ
ЃЈ2ЃЉЧѓЕуMЃЈxЃЌyЃЉдкКЏЪ§yЃНЉx+1ЕФЭМЯѓЩЯЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПзлКЯгыЪЕМљЃК
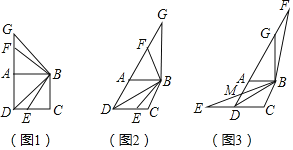
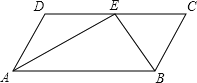
ЮЪЬтЧщОГЃКЃЈ1ЃЉШчЭМ1ЃЌЕуEЪЧе§ЗНаЮABCDБпCDЩЯЕФвЛЕуЃЌСЌНгBDЁЂBEЃЌНЋЁЯDBEШЦЕуBЫГеыа§зЊ90ЁуЃЌа§зЊКѓНЧЕФСНБпЗжБ№гыЩфЯпDAНЛгкЕуFКЭЕуGЃЎ
ЂйЯпЖЮBEКЭBFЕФЪ§СПЙиЯЕЪЧЁЁ ЁЁЃЛ
ЂкаДГіЯпЖЮDEЁЂDFКЭBDжЎМфЕФЪ§СПЙиЯЕЃЌВЂЫЕУїРэгЩЃЛ
ВйзїЬНОПЃКЃЈ2ЃЉдкСтаЮABCDжаЃЌЁЯADCЃН60ЁуЃЌЕуEЪЧСтаЮABCDБпCDЫљдкжБЯпЩЯЕФвЛЕуЃЌСЌНгBDЁЂBEЃЌНЋЁЯDBEШЦЕуBЫГЪБеыа§зЊ120ЁуЃЌа§зЊКѓНЧЕФСНБпЗжБ№гыЩфЯпDAНЛгкЕуFКЭЕуGЃЎ
ЂйШчЭМ2ЃЌЕуEдкЯпЖЮDCЩЯЪБЃЌЧыЬНОПЯпЖЮDEЁЂDFКЭBDжЎМфЕФЪ§СПЙиЯЕЃЌаДГіНсТлВЂИјГіжЄУїЃЎ
ЂкШчЭМ3ЃЌЕуEдкЯпЖЮCDЕФбгГЄЯпЩЯЪБЃЌBEНЛЩфЯпDAгкЕуMЃЌШєDEЃНDCЃН2aЃЌжБНгаДГіЯпЖЮFMКЭAGЕФГЄЖШЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
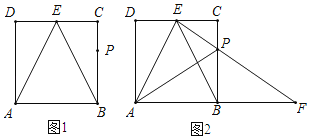
ЁОЬтФПЁПШчЭМ1ЃЌдкОиаЮABCDжаЃЌABЃН2ЃЌADЃН![]() ЃЌEЪЧCDБпЩЯЕФжаЕуЃЌPЪЧBCБпЩЯЕФвЛЕуЃЌЧвBPЃН2CPЃЎ
ЃЌEЪЧCDБпЩЯЕФжаЕуЃЌPЪЧBCБпЩЯЕФвЛЕуЃЌЧвBPЃН2CPЃЎ
ЃЈ1ЃЉЧѓжЄЃКЁЯAEDЃНЁЯBECЃЛ
ЃЈ2ЃЉХаЖЯEBЪЧЗёЦНЗжЁЯAECЃЌВЂЫЕУїРэгЩЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌСЌНгEPВЂбгГЄНЛABЕФбгГЄЯпгкЕуFЃЌСЌНгAPЃЌВЛЬэМгИЈжњЯпЃЌЁїPFBПЩвдгЩЖМОЙ§PЕуЕФСНДЮБфЛЛгыЁїPAEзщГЩвЛИіЕШбќШ§НЧаЮЃЌжБНгаДГіСНжжЗНЗЈЃЈжИГіЖдГЦжсЁЂа§зЊжааФЁЂа§зЊЗНЯђКЭЦНвЦОрРыЃЉЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдФЖСВФСЯЃК
аЁУїдкбЇЯАЖўДЮИљЪНКѓЃЌЗЂЯжвЛаЉКЌИљКХЕФЪНзгПЩвдаДГЩСэвЛИіЪНзгЕФЦНЗНЃЌШч![]() ЃЎЩЦгкЫМПМЕФаЁУїНјааСЫвдЯТЬНЫїЃК
ЃЎЩЦгкЫМПМЕФаЁУїНјааСЫвдЯТЬНЫїЃК
Щш![]() ЃЈЦфжа
ЃЈЦфжа![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ОљЮЊећЪ§ЃЉЃЌдђга
ОљЮЊећЪ§ЃЉЃЌдђга![]() ЃЎ
ЃЎ
![]() ЃЌ
ЃЌ![]() ЃЎетбљаЁУїОЭевЕНСЫвЛжжАбРрЫЦ
ЃЎетбљаЁУїОЭевЕНСЫвЛжжАбРрЫЦ![]() ЕФЪНзгЛЏЮЊЦНЗНЪНЕФЗНЗЈЃЎ
ЕФЪНзгЛЏЮЊЦНЗНЪНЕФЗНЗЈЃЎ
ЧыФуЗТееаЁУїЕФЗНЗЈЬНЫїВЂНтОіЯТСаЮЪЬтЃК
ЃЈ1ЃЉЕБ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ОљЮЊе§ећЪ§ЪБЃЌШє
ОљЮЊе§ећЪ§ЪБЃЌШє![]() ЃЌгУКЌ
ЃЌгУКЌ![]() ЁЂ
ЁЂ![]() ЕФЪНзгЗжБ№БэЪО
ЕФЪНзгЗжБ№БэЪО![]() ЁЂ
ЁЂ![]() ЃЌЕУЃК
ЃЌЕУЃК![]() ЁЁЁЁЃЌ
ЁЁЁЁЃЌ![]() ЁЁЁЁЃЛ
ЁЁЁЁЃЛ
ЃЈ2ЃЉРћгУЫљЬНЫїЕФНсТлЃЌеввЛзще§ећЪ§![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЬюПеЃКЁЁЁЁ
ЬюПеЃКЁЁЁЁ![]() ЁЁЁЁ
ЁЁЁЁ![]() ЁЁЁЁ
ЁЁЁЁ![]() ЁЁЁЁ
ЁЁЁЁ![]()
![]() ЃЛ
ЃЛ
ЃЈ3ЃЉШє![]() ЃЌЧв
ЃЌЧв![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ОљЮЊе§ећЪ§ЃЌЧѓ
ОљЮЊе§ећЪ§ЃЌЧѓ![]() ЕФжЕЃП
ЕФжЕЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊжБЯп![]() гыХзЮяЯп
гыХзЮяЯп![]() ЯрНЛгкAЃЌBСНЕуЃЌЧвЕуAЃЈ1ЃЌЃ4ЃЉЮЊХзЮяЯпЕФЖЅЕуЃЌЕуBдкxжсЩЯЁЃ
ЯрНЛгкAЃЌBСНЕуЃЌЧвЕуAЃЈ1ЃЌЃ4ЃЉЮЊХзЮяЯпЕФЖЅЕуЃЌЕуBдкxжсЩЯЁЃ

ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉдкЃЈ1ЃЉжаХзЮяЯпЕФЕкЖўЯѓЯоЭМЯѓЩЯЪЧЗёДцдквЛЕуPЃЌЪЙЁїPOBгыЁїPOCШЋЕШЃПШєДцдкЃЌЧѓГіЕуPЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЛ
ЃЈ3ЃЉШєЕуQЪЧyжсЩЯвЛЕуЃЌЧвЁїABQЮЊжБНЧШ§НЧаЮЃЌЧѓЕуQЕФзјБъЁЃ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊШёНЧ![]() ФкНггкЁбOЃЌ
ФкНггкЁбOЃЌ ![]() гкЕуDЃЌСЌНсAO.
гкЕуDЃЌСЌНсAO.
ЂХШє![]() .
.
ЂйЧѓжЄЃК![]() ЃЛ
ЃЛ
ЂкЕБ![]() ЪБЃЌЧѓ
ЪБЃЌЧѓ![]() УцЛ§ЕФзюДѓжЕЃЛ
УцЛ§ЕФзюДѓжЕЃЛ
ЂЦЕуEдкЯпЖЮOAЩЯЃЌ![]() ЃЌСЌНгDEЃЌЩш
ЃЌСЌНгDEЃЌЩш![]() ЃЌ
ЃЌ![]() ЃЈmЁЂnЪЧе§Ъ§ЃЉЃЌШє
ЃЈmЁЂnЪЧе§Ъ§ЃЉЃЌШє![]() ЃЌЧѓжЄЃК
ЃЌЧѓжЄЃК![]()

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃКШчЭМЃЌдкЫФБпаЮABCDжаЃЌADЁЮBCЃЎЕуEЮЊCDБпЩЯвЛЕуЃЌAEгыBEЗжБ№ЮЊЁЯDABКЭЁЯCBAЕФЦНЗжЯпЃЎ
ЃЈ1ЃЉЧыФуЬэМгвЛИіЪЪЕБЕФЬѕМўЁЁ ЁЁЃЌЪЙЕУЫФБпаЮABCDЪЧЦНааЫФБпаЮЃЌВЂжЄУїФуЕФНсТлЃЛ
ЃЈ2ЃЉзїЯпЖЮABЕФДЙжБЦНЗжЯпНЛABгкЕуOЃЌВЂвдABЮЊжБОЖзїЁбOЃЈвЊЧѓЃКГпЙцзїЭМЃЌБЃСєзїЭМКлМЃЃЌВЛаДзїЗЈЃЉЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌЁбOНЛБпADгкЕуFЃЌСЌНгBFЃЌНЛAEгкЕуGЃЌШєAE=4ЃЌsinЁЯAGF=![]() ЃЌЧѓЁбOЕФАыОЖЃЎ
ЃЌЧѓЁбOЕФАыОЖЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШєЪ§aЪЙЙигкxЕФЗжЪНЗНГЬ![]() =4ЕФНтЮЊе§Ъ§ЃЌЧвЪЙЙигкyЃЌВЛЕШЪНзщ
=4ЕФНтЮЊе§Ъ§ЃЌЧвЪЙЙигкyЃЌВЛЕШЪНзщ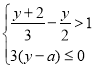 ЕФНтМЏЮЊyЃМ-2ЃЌдђЗћКЯЬѕМўЕФЫљгаећЪ§aЕФКЭЮЊ______ЃЎ
ЕФНтМЏЮЊyЃМ-2ЃЌдђЗћКЯЬѕМўЕФЫљгаећЪ§aЕФКЭЮЊ______ЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com