
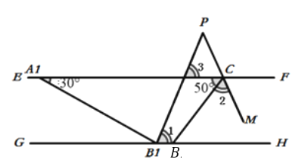
【题目】如图①,已知直线EF∥GH,点A、C在直线EF上,点B在直线GH上,连接AB、BC,∠ACB=50°,∠BAC=30°,BP平分∠ABH,CM平分∠BCF,BP与CM的反向延长线相交于P.
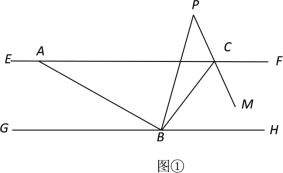
(1)求∠BPC的度数;
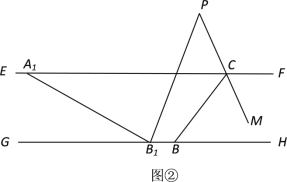
(2)若将图①中的线段AB沿EF向左平移到A1B1,如图②所示位置,此时B1P平分∠A1B1H,CM平分∠BCF,B1P与CM的反向延长线相交于P,求∠B1PC的度数.
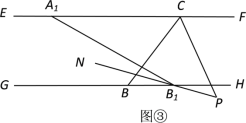
(3)若将图①中的线段AB沿EF向右平移到A1B1,如图③所示位置,此时B1N平分∠A1B1B,CP平分∠BCF, CP与B1N的反向延长线相交于P,求∠B1PC的度数.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)利用平行线的性质、角平分线的性质可求得![]() 和
和![]() ,根据三角形外角的性质可求解;
,根据三角形外角的性质可求解;
(2)利用平行线的性质、角平分线的性质、三角形外角的性质可求解;
(3)利用平行线的性质、角平分线的性质、三角形外角的性质可求解.
(1)如图:∵EF∥GH,∠BAC=30°,BP平分∠ABH,
∴![]() ,
,
∵EF∥GH,∠ACB=50°,CM平分∠BCF,
∴![]() ,
,
∵EF∥GH,∠ACB=50°,
∴![]()
∴![]()
![]()
∴![]() ;
;
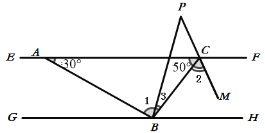
(2)如图:∵EF∥GH,∠![]() AC=30°,
AC=30°,![]() P平分∠
P平分∠![]() H,
H,
∴![]() ,
,
∵EF∥GH,∠ACB=50°,CM平分∠BCF,
∴![]() ,
,
![]()
∴![]() ;
;
(3)如图:∵EF∥GH,∠![]() AC=30°,
AC=30°,![]() P平分∠
P平分∠![]() B,
B,
∴![]() ,
,
∵EF∥GH,∠ACB=50°,CP平分∠BCF,
∴![]() ,
,
![]()
∴![]() ;
;


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】在一次中学生田径运动会上,根据参加男子跳高初赛的运动员的成绩(单位:m),绘制出如下的统计图①和图②.请根据相关信息,解答下列问题:
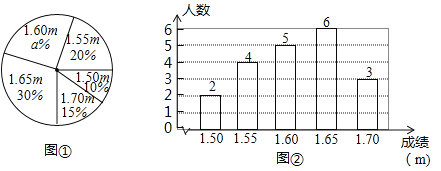
(Ⅰ)图①中![]() 的值为__________;
的值为__________;
(Ⅱ)求统计的这组初赛成绩数据的平均数、众数和中位数;
(Ⅲ)根据这组初赛成绩,由高到低确定10人能进入复赛,请直接写出初赛成绩为![]() 的运动员能否进入复赛.
的运动员能否进入复赛.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017年12月,旗团委号召各校组织开展捐赠衣物的“暖冬行动”![]() 某校七年级六个班参加了这次捐赠活动,若每班捐赠衣物以100件为基准,超过的件数用正数表示,不足的件数用负数表示,记录如下:
某校七年级六个班参加了这次捐赠活动,若每班捐赠衣物以100件为基准,超过的件数用正数表示,不足的件数用负数表示,记录如下:
班级 | 一班 | 二班 | 三班 | 四班 | 五班 | 六班 |
人数 | 40 | 43 | 45 | 44 | 40 | 38 |
件数 |
|
|
|
|
|
|
![]() 捐赠衣物最多的班比最少的班多多少件?
捐赠衣物最多的班比最少的班多多少件?
![]() 该校七年级学生共捐赠多少件衣物?该校七年级学生平均每人捐赠多少件衣物?
该校七年级学生共捐赠多少件衣物?该校七年级学生平均每人捐赠多少件衣物?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,![]() ,
,![]() 是
是![]() 的中点,
的中点,![]() ,垂足为点
,垂足为点![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() 是
是![]() 边上一动点,设
边上一动点,设![]() 的长为
的长为![]() .
.
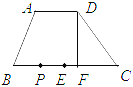
(1)当![]() 的值为________或________时,以点
的值为________或________时,以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形为平行四边形.
为顶点的四边形为平行四边形.
(2)点![]() 在
在![]() 边上运动的过程中,以
边上运动的过程中,以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形能否构成菱形?试说明理由.
为顶点的四边形能否构成菱形?试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD对角线BD上截取BE=BC,连接CE并延长交AD于点F,连接AE,过B作BG⊥AE于点G,交AD于点H,则下列结论错误的是( )
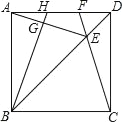
A. AH=DF B. S四边形EFHG=S△DCF+S△AGH
C. ∠AEF=45° D. △ABH≌△DCF
查看答案和解析>>
科目:初中数学 来源: 题型:
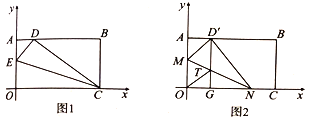
【题目】将一矩形纸片![]() 放在直角坐标系中,
放在直角坐标系中,![]() 为原点,点
为原点,点![]() 在
在![]() 轴上,点
轴上,点![]() 在
在![]() 轴上,
轴上,![]() .
.
(1)如图1,在![]() 上取一点
上取一点![]() ,将
,将![]() 沿
沿![]() 折叠,使
折叠,使![]() 点落在
点落在![]() 边上的
边上的![]() 点处,求直线
点处,求直线![]() 的解析式;
的解析式;
(2)如图2,在![]() 边上选取适当的点
边上选取适当的点![]() ,将
,将![]() 沿
沿![]() 折叠,使
折叠,使![]() 点落在
点落在![]() 边上的点
边上的点![]() 处,过
处,过![]() 作
作![]() 于点
于点![]() ,交
,交![]() 于
于![]() 点,连接
点,连接![]() ,判断四边形
,判断四边形![]() 的形状,并说明理由;
的形状,并说明理由;
(3)、在(2)的条件下,若点![]() 坐标
坐标![]() ,点
,点![]() 在
在![]() 直线上,问坐标轴上是否存在点
直线上,问坐标轴上是否存在点![]() ,使以
,使以![]() 为顶点的四边形是平行四边形,若存在,请直接写出点
为顶点的四边形是平行四边形,若存在,请直接写出点![]() 坐标;若不存在,请说明理由.
坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市粮店出售某种大米,上半月的售价为每公斤![]() 元,下半月的售价为每公斤
元,下半月的售价为每公斤![]() 元.有一餐饮业老板每个月要向该店采购两次大米,且上半月购买一次,下半月购买一次.该老板结合市场米价情况,设计两套采购方案:A.每次购买100公斤大米;B.每次购买100元钱的大米.请你运用所学知识分析一下,该老板采用哪种方式购买较划算.
元.有一餐饮业老板每个月要向该店采购两次大米,且上半月购买一次,下半月购买一次.该老板结合市场米价情况,设计两套采购方案:A.每次购买100公斤大米;B.每次购买100元钱的大米.请你运用所学知识分析一下,该老板采用哪种方式购买较划算.
查看答案和解析>>
科目:初中数学 来源: 题型:
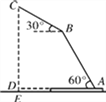
【题目】放置在水平桌面上的台灯的灯臂AB长为40 cm,灯罩BC长为30 cm,底座厚度为2 cm,灯臂与底座构成的∠BAD=60°.使用发现,光线最佳时灯罩BC与水平线所成的角为30°,此时灯罩顶端C到桌面的高度CE是多少厘米?(结果精确到0.1 cm,参考数据:![]() ≈1.732)
≈1.732)

查看答案和解析>>
科目:初中数学 来源: 题型:
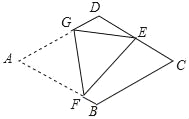
【题目】如图,在菱形纸片ABCD中,AB=3,∠A=60°,将菱形纸片翻折,使点A落在CD的中点E处,折痕为FG,点F,G分别在边AB,AD上,则tan∠EFG的值为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com