
【题目】已知正方形ABCD的边长为1,点P为正方形内一动点,若点M在AB上,且满足△PBC∽△PAM,延长BP交AD于点N,连结CM.
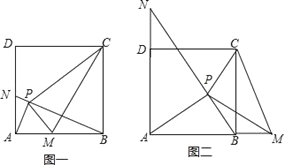
(1)如图一,若点M在线段AB上,求证:AP⊥BN;AM=AN;
(2)①如图二,在点P运动过程中,满足△PBC∽△PAM的点M在AB的延长线上时,AP⊥BN和AM=AN是否成立?
②是否存在满足条件的点P,使得PC=![]() ?(不需说明理由).
?(不需说明理由).
【答案】(1)证明见解析;(2)①仍然成立,AP⊥BN和AM=AN. ②这样的点P不存在.
【解析】试题分析:(1)根据相似三角形的性质得到∠PAM=∠PBC,根据正方形的性质证明,得到AP⊥BN,根据相似三角形的对应边的比线段求出AM与AN的数量关系;
(2)①同(1)的证明方法类似;
②根据圆周角定理得到点P在以AB为直径的圆上,根据勾股定理计算即可.
试题解析:(1)如图一中,∵四边形ABCD是正方形,∴AB=BC=CD=AD,∠DAB=∠ABC=∠BCD=∠D=90°,
∵△PBC∽△PAM,∴∠PAM=∠PBC, ![]() ,∴∠PBC+∠PBA=90°,∴∠PAM+∠PBA=90°,
,∴∠PBC+∠PBA=90°,∴∠PAM+∠PBA=90°,
∴∠APB=90°,∴AP⊥BN,∵∠ABP=∠ABN,∠APB=∠BAN=90°,
∴△BAP∽△BNA,∴![]() ,∴
,∴![]() ,∵AB=BC,∴AN=AM.
,∵AB=BC,∴AN=AM.
(2)①仍然成立,AP⊥BN和AM=AN.
理由如图二中,∵四边形ABCD是正方形,∴AB=BC=CD=AD,∠DAB=∠ABC=∠BCD=∠D=90°,
∵△PBC∽△PAM, ∴∠PAM=∠PBC, ![]() ,∴∠PBC+∠PBA=90°,
,∴∠PBC+∠PBA=90°,
∴∠PAM+∠PBA=90°, ∴∠APB=90°,∴AP⊥BN,∵∠ABP=∠ABN,∠APB=∠BAN=90°,
∴△BAP∽△BNA,∴![]() ,∴
,∴![]() ,∵AB=BC,∴AN=AM.
,∵AB=BC,∴AN=AM.
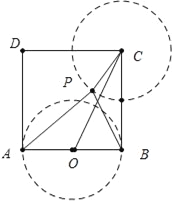
②这样的点P不存在.理由:假设PC=![]() ,如图三中,以点C为圆心
,如图三中,以点C为圆心![]() 为半径画圆,以AB为直径画圆, CO=
为半径画圆,以AB为直径画圆, CO=![]() =
=![]() >1+
>1+![]() ,∴两个圆无公共点,∴∠APB<90°,这与AP⊥PB矛盾,
,∴两个圆无公共点,∴∠APB<90°,这与AP⊥PB矛盾,
∴假设不可能成立,∴满足PC=![]() 的点P不存在.
的点P不存在.


科目:初中数学 来源: 题型:
【题目】嘉淇同学要证明命题“两组对边分别相等的四边形是平行四边形”是正确的,她先用尺规作出了如图1的四边形ABCD,并写出了如下不完整的已知和求证.
已知:如图1,在四边形ABCD中,BC=AD,
求证:四边形ABCD是四边形.
(1)在方框中填空,以补全已知和求证;
(2)按嘉淇的想法写出证明;
(3)用文字叙述所证命题的逆命题为平行四边形两组对边分别相等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“明天的降水概率为90%”的含义解释正确的是( )
A.明天90%的地区会下雨B.90%的人认为明天会下雨
C.明天90%的时间会下雨D.在100次类似于明天的天气条件下,大约有90次会下雨
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数 y=ax2+bx+c(a≠0)的图象的一部分,给出下列命题:①a+b+c=0;②b>2a;③ax2+bx+c=0的两根分别为-3和1;④a-2b+c>0.其中正确的命题是( )
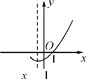
A. ①② B. ②③ C. ①③ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
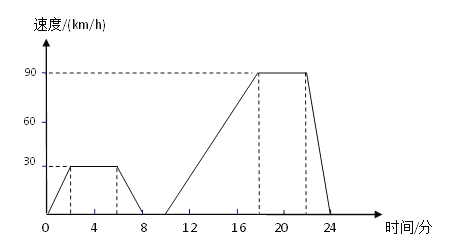
【题目】如图表示的是汽车在行驶的过程中,速度随时间变化而变化的情况.
(1)汽车从出发到最后停止共经过了多少时间?它的最高时速是多少?
(2)汽车在那些时间段保持匀速行驶?时速分别是多少?
(3)出发后8分到10分之间可能发生了什么情况?
(4)用自己的语言大致描述这辆汽车的行驶情况.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com