
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 我国是世界上严重缺水的国家之一.为了增强居民的节水意识,某市自来水公司对居民用水采用以户为单位分段计费的办法收费.即一个月用水10吨以内(包括10吨)的用户,每吨收水费a元;一个月用水超过10吨的用户,10吨水仍按每吨a元收费,超过10吨的部分,按每吨b元(b>a)收费.设一户居民月用水x吨,应收水费y元,y与x之间的函数关系如图:
我国是世界上严重缺水的国家之一.为了增强居民的节水意识,某市自来水公司对居民用水采用以户为单位分段计费的办法收费.即一个月用水10吨以内(包括10吨)的用户,每吨收水费a元;一个月用水超过10吨的用户,10吨水仍按每吨a元收费,超过10吨的部分,按每吨b元(b>a)收费.设一户居民月用水x吨,应收水费y元,y与x之间的函数关系如图:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
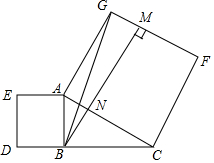 如图,在Rt△ABC中,∠ABC=90°,分别以AB、AC为边向外作正方形ABDE和正方形ACFG,过点B作BM⊥GF,垂足为M,BM交AC于点N,连接BG,CE,下列结论中,不正确的是( )
如图,在Rt△ABC中,∠ABC=90°,分别以AB、AC为边向外作正方形ABDE和正方形ACFG,过点B作BM⊥GF,垂足为M,BM交AC于点N,连接BG,CE,下列结论中,不正确的是( )| A. | BG=CE | B. | BG⊥CE | ||
| C. | S正方形ABDE>S四边形ANMG | D. | BC2=CF•FM |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com