
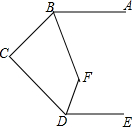
 如图,已知AB∥DE,BC⊥CD,∠ABC和∠CDE的平分线交于点F,∠BFD=135°.
如图,已知AB∥DE,BC⊥CD,∠ABC和∠CDE的平分线交于点F,∠BFD=135°. 分析 连接BD,再根据三角形内角和定理得出∠C+∠CBD+∠CDB=180°,再由BC⊥CD可知∠C=90°,故∠CBD+∠CDB=90°,再由AB∥DE可知∠ABD+∠CDE=180°,故∠CBD+∠CDB+∠ABD+∠CDE=90°+180°=270°,再由∠ABC和∠CDE的平分线交于点F可得出∠CBF+∠CDF的度数,由四边形内角和定理即可得出结论.
解答  解:连接BD,
解:连接BD,
∵∠C+∠CBD+∠CDB=180°,BC⊥CD,
∴∠C=90°,
∴∠CBD+∠CDB=90°.
∵AB∥DE,
∴∠ABD+∠CDE=180°,
∴∠CBD+∠CDB+∠ABD+∠CDE=90°+180°=270°,即∠ABC+∠CDE=270°.
∵∠ABC和∠CDE的平分线交于点F,
∴∠CBF+∠CDF=$\frac{1}{2}$×270°=135°,
∴∠BFD=360°-90°-135°=135°.
故答案为:135.
点评 本题考查的是平行线的性质,根据题意作出辅助线,构造出三角形是解答此题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 为了让更多的失学儿童重返校园,某社区组织“献爱心手拉手”捐款活动,对社区部分捐款户数进行调查和分组统计后,将数据整理成如图所示的统计表和统计图(图中信息不完整).已知A、B两组捐款户数的比为1:5.
为了让更多的失学儿童重返校园,某社区组织“献爱心手拉手”捐款活动,对社区部分捐款户数进行调查和分组统计后,将数据整理成如图所示的统计表和统计图(图中信息不完整).已知A、B两组捐款户数的比为1:5.| 组别 | 捐款额(x)元 | 户数 |
| A | 1≤x<50 | a |
| B | 50≤x<100 | 10 |
| C | 100≤x<150 | |
| D | 150≤x<200 | |
| E | x≥200 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 相等的角是对顶角 | B. | 两点之间线段最短 | ||
| C. | 两直线平行,同旁内角相等 | D. | 若$\sqrt{{a}^{2}}$=a,则a>0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com