如图.在平面直角坐标系中.直线y=x+4与抛物线y=ax2-3x+c交于A.B两点.点A在x轴上.点B在y轴上．(1)求抛物线的解析式,(2)点P是直线AB上方的抛物线上一动点.且位于该抛物线对称轴左侧.过点P作PQ∥y轴.交直线AB于点Q.作矩形PQCD.使点D落在抛物线上.设矩形PQCD的周长为l.点P的横坐标为m.求l关于m的函数关系式.并求出l的最大值,中的取l最大值时.设� 题目和参考答案——青夏教育精英家教网—

16．

如图，在平面直角坐标系中，直线y=x+4与抛物线y=ax²-3x+c交于A、B两点，点A在x轴上，点B在y轴上．
（1）求抛物线的解析式；
（2）点P是直线AB上方的抛物线上一动点，且位于该抛物线对称轴左侧，过点P作PQ∥y轴，交直线AB于点Q，作矩形PQCD，使点D落在抛物线上，设矩形PQCD的周长为l，点P的横坐标为m，求l关于m的函数关系式，并求出l的最大值；
（3）在（2）中的取l最大值时，设点E是线段OA上一动点，连接PE，过点E作EF⊥PE交y轴于点F，若点F的坐标为（0，k），请直接写出k的取值范围．

分析（1）根据直线方程得到点A、B的坐标，然后将其分别代入抛物线方程，列出关于a、c的方程组，通过解该方程组求得系数a、c的值；
（2）由二次函数图象上点的坐标特征求得P点的坐标，根据点Q在直线AB上可以推知点Q的坐标；由抛物线的对称性得到点D的坐标；结合该矩形的周长公式求l关于m的函数关系式，并由配方法求出l的最大值；
（3）求出P点坐标，根据点E与点A重合时k的值最小，当点E在线段OA的中点时k最大即可得出结论．

解答解：（1）∵A、B是直线y=x+4上的点，
∴A（-4，0），B（0，4）．
∵抛物线y=ax²-3x+c经过A、B两点，
∴$\left\{\begin{array}{l}16a+12+c=0\\ c=4\end{array}\right.$，
解得$\left\{\begin{array}{l}a=-1\\ c=4\end{array}\right.$．
∴抛物线的解析式为y=-x²-3x+4；

（2）∵点P的横坐标为m，
∴P（m，-m²-3m+4），Q（m，m+4）．
∵抛物线的解析式为y=-x²-3x+4，
∴抛物线的对称轴为x=-$\frac{-3}{-2}$=-$\frac{3}{2}$．
∵PD两点关于直线x=-$\frac{3}{2}$对称，
∴D（-3-m，-m²-3m+4），
∴PQ=-m²-3m+4-（m+4）=-m²-3m+4-m-4=-m²-4m，PD=-3-m-m=-3-2m，
∴l=2（PQ+PD）=2（-m²-4m-3-2m）=2（-m²-6m-3）=-2m²-12m-6，
∴当m=-$\frac{-12}{2×（-2）}$=-3时，l_最大=12；

（3）∵由（2）知当m=-3时l最大，
∴P（-3，4）．
设直线PA的解析式为y=ax+b（a≠0），
∵A（-4，0），
∴$\left\{\begin{array}{l}-3a+b=4\\-4a+b=0\end{array}\right.$，
解得$\left\{\begin{array}{l}a=4\\ b=16\end{array}\right.$．
∴直线PA的解析式为y=4x+16．
∵当点A与点E重合时直线PE的解析式为y=4x+16．
∵EF⊥PE，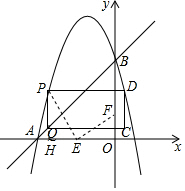
∴设直线EF的解析式为y=-$\frac{1}{4}$x+c，
∴1+c=0，解得c=-1，
∴直线EF的解析式为y=-$\frac{1}{4}$x-1，
延长PQ交x轴于点H，则H的坐标是（-3，0），
当E在PH的右边，设E的坐标是（e，0），
∵∠PEF=90°，PH⊥⊥x轴．
∴∠PEH+∠FEO=90°，∠PEH+∠EPH=90°，
∴∠PEH=∠FEO，
又∵∠PHE=∠EOF，
∴△PEH∽△EFO，
∴$\frac{PH}{OE}$=$\frac{EH}{OF}$，即$\frac{4}{-e}$=$\frac{e+3}{k}$，
∴k=-$\frac{1}{4}$e²-$\frac{3}{4}$e．
当e=-$\frac{-\frac{3}{4}}{2×（-\frac{1}{4}）}$=-$\frac{3}{2}$时，k=$\frac{9}{16}$．
∴-1≤k≤$\frac{9}{16}$．

点评本题考查的是二次函数综合题，涉及到二次函数图象上点的坐标特点、二次函数与一次函数的交点问题等知识，难度较大．

练习册系列答案