
【题目】课题:两个重叠的正多边形,其中的一个绕某一顶点旋转所形成的有关问题.
实验与论证:
设旋转角∠A1A0B1=α(α<∠A1A0A2),θ3、θ4、θ5、θ6所表示的角如图所示.
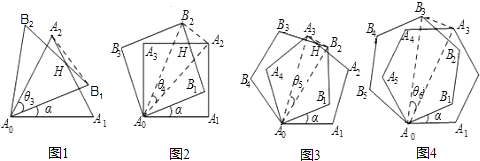
(1)用含α的式子表示角的度数:θ3= ,θ4= ,θ5= ;
(2)图1﹣图4中,连接A0H时,在不添加其他辅助线的情况下,是否存在与直线A0H垂直且被它平分的线段?若存在,请选择其中的一个图给出证明;若不存在,请说明理由;
归纳与猜想:
设正n边形A0A1A2…An﹣1与正n边形A0B1B2…Bn﹣1重合(其中,A1与B1重合),现将正多边形A0B1B2…Bn﹣1绕顶点A0逆时针旋转α(0°<α<![]() °);
°);
(3)设θn与上述“θ3、θ4、…”的意义一样,请直接写出θn的度数;
(4)试猜想在正n边形的情形下,是否存在与直线A0H垂直且被它平分的线段?若存在,请将这条线段用相应的顶点字母表示出来(不要求证明);若不存在,请说明理由.
【答案】(1)60°﹣α,α,36°﹣α;(2)存在,证明见详解;(3)当n为奇数时,θn=![]() ﹣α;当n为偶数时,θn=α;(4)存在.当n为奇数时,直线A0H垂直平分
﹣α;当n为偶数时,θn=α;(4)存在.当n为奇数时,直线A0H垂直平分![]() ,当n为偶数时,直线A0H垂直平分
,当n为偶数时,直线A0H垂直平分![]()
【解析】
(1)由正三角形的性质得α+θ3=60°,再由正方形的性质得θ4=45°﹣(45°﹣α)=α,最后由正五边形的性质得θ5=108°﹣36°﹣36°﹣α=36°﹣α;
(2)存在,如在图1中直线A0H垂直且平分的线段A2B1,△A0A1A2≌△A0B1B2,推得A2H=B1H,则点H在线段A2B1的垂直平分线上;由A0A2=A0B1,则点A0在线段A2B1的垂直平分线上,从而得出直线A0H垂直且平分的线段A2B1
(3)当n为奇数时,θn=![]() ﹣α;
﹣α;
当n为偶数时,θn=α
(4)多写几个总结规律:
当n为奇数时,直线A0H垂直平分![]() ,
,
当n为偶数时,直线A0H垂直平分![]() .
.
解:(1) ∵三角形的性质得α+θ3=60°,
∴θ3=60°﹣α,
由正方形的性质得θ4=45°﹣(45°﹣α)=α,
由正五边形的性质得θ5=108°﹣36°﹣36°﹣α=36°﹣α,
故答案为60°﹣α;α;36°﹣α;
(2)存在.下面就所选图形的不同分别给出证明:
选图如,
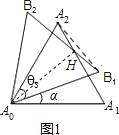
图中有直线A0H垂直平分A2B1,证明如下:
方法一:
证明:∵△A0A1A2与△A0B1B2是全等的等边三角形
∴A0A2=A0B1
∴∠A0A2B1=∠A0B1A2,
又∠A0A2H=∠A0B1H=60°
∴∠HA2B1=∠HB1A2
∴A2H=B1H,∴点H在线段A2B1的垂直平分线上
又∵A0A2=A0B1,∴点A0在线段A2B1的垂直平分线上
∴直线A0H垂直平分A2B1
方法二:
证明:∵△A0A1A2与△A0B1B2是全等的等边三角形
∴A0A2=A0B2,
∴∠A0A2B1=∠A0B1A2,
又∠A0A2H=∠A0B1H=60°,
∴∠HA2B1=∠HB1A2
∴A2H=B1H,
在△A0A2H与△A0B1H中
∵A0A2=A0B1,
HA2=HB1,∠A0A2H=∠A0B1H
∴△A0A2H≌△A0B1H
∴∠A0A2H=∠A0B1H,
∴A0H是等腰三角形A0A2B1的角平分线,
∴直线A0H垂直平分A2B1选图如,
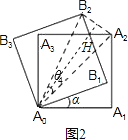
图中有直线A0H垂直平分A2B2,证明如下:
∵A0B2=A0A2∴∠A0B2A2=∠A0A2B2
又∵∠A0B2B1=∠A0A2A3
∴∠HB2A2=∠HA2B2
∴HB2=HA2
∴点H在线段A2B2的垂直平分线上
又∵A0B2=A0A2,∴点A0在线段A2B2的垂直平分线上
∴直线A0H垂直平分A2B2
(3)当n为奇数时,θn=![]() ﹣α;
﹣α;
当n为偶数时,θn=α.
(4)存在.
当n为奇数时,直线A0H垂直平分![]() ,
,
当n为偶数时,直线A0H垂直平分![]()


科目:初中数学 来源: 题型:
【题目】一个不透明的布袋中有完全相同的三个小球,把它们分别标号为1,2,3. 小林和小华做一个游戏,按照以下方式抽取小球:先从布袋中随机抽取一个小球,记下标号后放回布袋中搅匀,再从布袋中随机抽取一个小球, 记下标号. 若两次抽取的小球标号之和为奇数,小林赢;若标号之和为偶数,则小华赢.
(1)用画树状图或列表的方法,列出前后两次取出小球上所标数字的所有可能情况;
(2)请判断这个游戏是否公平,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AB是⊙O的直径,C为⊙O上一点,∠OAC=58°.

(Ⅰ)如图①,过点C作⊙O的切线,与BA的延长线交于点P,求∠P的大小;
(Ⅱ)如图②,P为AB上一点,CP延长线与⊙O交于点Q.若AQ=CQ,求∠APC的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
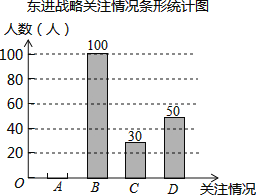
【题目】深圳市政府计划投资1.4万亿元实施东进战略.为了解深圳市民对东进战略的关注情况.某校数学兴趣小组随机采访部分深圳市民,对采访情况制作了统计图表的一部分如下:
关注情况 | 频数 | 频率 |
A.高度关注 | m | 0.1 |
B.一般关注 | 100 | 0.5 |
C.不关注 | 30 | n |
D.不知道 | 50 | 0.25 |
(1)根据上述统计图可得此次采访的人数为 人,m= ,n= ;
(2)根据以上信息补全条形统计图;
(3)根据上述采访结果,请估计在15000名深圳市民中,高度关注东进战略的深圳市民约有 人.
查看答案和解析>>
科目:初中数学 来源: 题型:
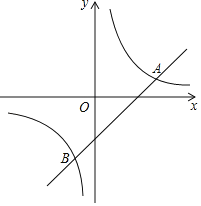
【题目】如图,在平面直角坐标系xOy中,直线y=x﹣2与双曲线y=![]() (k≠0)相交于A,B两点,且点A的横坐标是3.
(k≠0)相交于A,B两点,且点A的横坐标是3.
(1)求k的值;
(2)过点P(0,n)作直线,使直线与x轴平行,直线与直线y=x﹣2交于点M,与双曲线y=![]() (k≠0)交于点N,若点M在N右边,求n的取值范围.
(k≠0)交于点N,若点M在N右边,求n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某教室的开关控制板上有四个外形完全相同的开关,其中两个分别控制A、B两
盏电灯,另两个分别控制C、D两个吊扇.已知电灯、吊扇均正常,且处于不工作状态,开
关与电灯、电扇的对应关系未知.
(1)若四个开关均正常,则任意按下一个开关,正好一盏灯亮的概率是多少?
(2)若其中一个控制电灯的开关坏了,则任意按下两个开关,正好一盏灯亮和一个扇转的概率是多少?请用树状图法或列表法加以说明
查看答案和解析>>
科目:初中数学 来源: 题型:
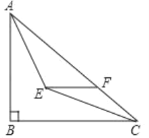
【题目】如图,在Rt△ABC中,∠ABC=90°,AB=6,BC=8,∠BAC,∠ACB的平分线相交于点E,过点E作EF∥BC交AC于点F,则EF的长为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了提高学生的阅读能力,我市某校开展了“读好书,助成长”的活动,并计划购置一批图书,购书前,对学生喜欢阅读的图书类型进行了抽样调查,并将调查数据绘制成两幅不完整的统计图,如图所示,请根据统计图回答下列问题:
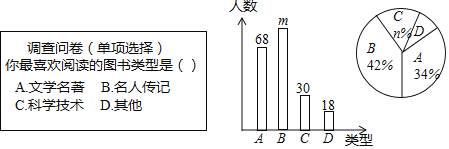
(1)本次调查共抽取了 名学生,两幅统计图中的m= ,n= .
(2)已知该校共有3600名学生,请你估计该校喜欢阅读“A”类图书的学生约有多少人?
(3)学校将举办读书知识竞赛,九年级1班要在本班3名优胜者(2男1女)中随机选送2人参赛,请用列表或画树状图的方法求被选送的两名参赛者为一男一女的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com