
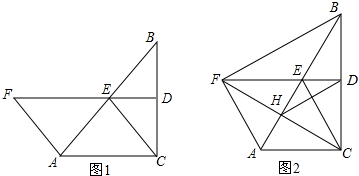
分析 (1)由已知条件易证AF=CE,再证明CE∥AF,即可证明四边形ACEF是平行四边形;
(2)根据菱形的性质以及等边三角形的判定方法即可写出所有等边三角形.
解答 (1)证明:∵∠ACB=90°,E是BA的中点,
∴CE=AE,
∵AF=AE,
∴AF=CE,
∵ED平分∠BEC,
∴∠1=∠2,
∵AF=AE,
∴∠F=∠3,
∵∠1=∠3,
∴∠2=∠F,
∴CE∥AF,
又∵CE=AF,
∴四边形ACEF是平行四边形;
(2)解:△AFE,△AEC,△HDC,△CFB.
点评 此题考查了菱形的性质、平行四边形的判定和性质以及等边三角形的判定与性质.题目的综合性较强,具有一定难度,解题的关键是熟记特殊几何图形的判定方法以及其性质.


科目:初中数学 来源: 题型:填空题
 如图,在同一平面内,圆O和直线AB相切,P是圆O上一个定点,初始位置圆O和AB相切于点A(此时点P与点A重合),从A处开始圆O在直线AB上以每3分钟1圈的速度匀速向右无滑动地滚动,1分钟到达点E(圆O与AB相切于点E),此时,tan∠PAE的值为$\frac{9}{4π-3\sqrt{3}}$.
如图,在同一平面内,圆O和直线AB相切,P是圆O上一个定点,初始位置圆O和AB相切于点A(此时点P与点A重合),从A处开始圆O在直线AB上以每3分钟1圈的速度匀速向右无滑动地滚动,1分钟到达点E(圆O与AB相切于点E),此时,tan∠PAE的值为$\frac{9}{4π-3\sqrt{3}}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 甲车从A地出发,途径C地时休息一小时,然后按原速度继续前进到达B地;乙车从C地出发到B地后又按原速返回C地,两车同时出发,并以各自的速度匀速行驶,设A,C,B在同一条直线上,如图是甲、乙两车和B地的距离y(千米)与甲车出发时间x(小时)的函数图象.
甲车从A地出发,途径C地时休息一小时,然后按原速度继续前进到达B地;乙车从C地出发到B地后又按原速返回C地,两车同时出发,并以各自的速度匀速行驶,设A,C,B在同一条直线上,如图是甲、乙两车和B地的距离y(千米)与甲车出发时间x(小时)的函数图象.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
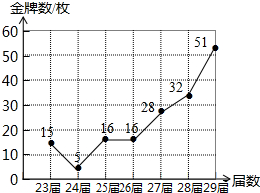 从1984年起,我国先后参加了第23届夏季奥运会,取得了骄人的成绩.如图是根据第23届至29届夏季奥运会我国获得的金牌数绘制的折线统计图,观察统计图可得:与上一届相比增长量最大的是第29届夏季奥运会,比它的上一届增加了19枚金牌.
从1984年起,我国先后参加了第23届夏季奥运会,取得了骄人的成绩.如图是根据第23届至29届夏季奥运会我国获得的金牌数绘制的折线统计图,观察统计图可得:与上一届相比增长量最大的是第29届夏季奥运会,比它的上一届增加了19枚金牌.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
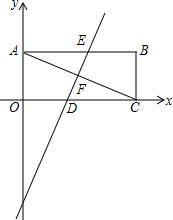 如图,平面直角坐标系中,矩形OABC的两条邻边分别在x轴、y轴上,对角线AC=4$\sqrt{5}$,边OA=4.
如图,平面直角坐标系中,矩形OABC的两条邻边分别在x轴、y轴上,对角线AC=4$\sqrt{5}$,边OA=4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知BC为半圆O的直径,AD⊥BC,垂足为D,过点B作弦BF交AD于E,交半圆O于点F,弦AC与BF交于点H,且AE=BE,
已知BC为半圆O的直径,AD⊥BC,垂足为D,过点B作弦BF交AD于E,交半圆O于点F,弦AC与BF交于点H,且AE=BE,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com