
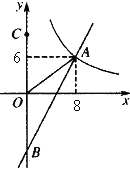
【题目】如图,一次函数y=kx+b的图象分别与反比例函数![]() 的图象在第一象限交于点A(8,6),与y轴的负半轴交于点B,且OA=OB.
的图象在第一象限交于点A(8,6),与y轴的负半轴交于点B,且OA=OB.
(1)求函数y=kx+b和![]() 的表达式;
的表达式;
(2)已知点C(0,10),试在该一次函数图象上确定一点M,使得MB=MC。求此时点M的坐标.
【答案】(1)y=2x-10;(2)M(5,0)
【解析】分析:(1)、根据点A的坐标求出反比例函数的解析式,然后根据OA=OB得出点B的坐标,最后根据点A和点B的坐标求出一次函数的解析式;(2)、根据MB=MC得出点M在线段BC的中垂线上,从而得出点的坐标.
详解:解(1):将A(8,6)代入![]() , 得
, 得![]() ,∴a=48,∴反比例函数为
,∴a=48,∴反比例函数为![]() ,
,
∵OA=10,由于OA=OB,且B在y轴负半轴上,∴B(0,-10)
将A(8,6),B(0,-10)代入y=kx+b
得:![]() ,∴
,∴![]() ,∴y=2x-10
,∴y=2x-10
(2)∵MB=MC,∴M在线段BC的中垂线上,即x轴上,
∴M为一次函数图象与 x轴交点,令2x-10=0,∴x=5,∴M(5,0).


 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案科目:初中数学 来源: 题型:
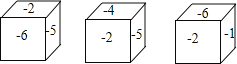
【题目】一个正方体的六个面上分别标有﹣1,﹣2,﹣3,﹣4,﹣5,﹣6中的一个数,各个面上所标数字都不相同,如图是这个正方体的三种放置方法,三个正方体下底面所标数字分别是a,b,c,则a+b+c+abc=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)﹣3.25﹣(﹣19)+(﹣6.75)+179
(2)116﹣(﹣40+100)+2(15﹣27)
(3)(﹣9)÷(![]() )×(
)×(![]() )
)
(4)﹣14+16÷(﹣2)3×|﹣3﹣1|﹣1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋里装有分别标有汉字“美”、“丽”、“泰”、“兴”的四个小球,除汉字不同之外,小球没有任何区别,每次摸球前先搅拌均匀再摸球.
(1)若从中任取一个球,求摸出球上的汉字刚好是“美”的概率;
(2)甲从中任取一球,不放回,再从中任取一球,请用树状图或列表法,求甲取出的两个球上的汉字恰能组成“美丽”或“泰兴”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面内有任意一点![]() 和
和![]() ,按要求解答下列问题:
,按要求解答下列问题:
(1)当点![]() 和
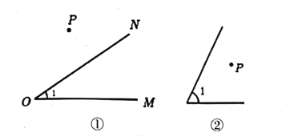
和![]() 外部时,如图①,过点
外部时,如图①,过点![]() 作
作![]() ,
,![]() ,垂足分别为
,垂足分别为![]() 、
、![]() ,量一量
,量一量![]() 和
和![]() 的度数,用数学式子表达它们之间的数量关系 ;
的度数,用数学式子表达它们之间的数量关系 ;
(2)当点![]() 在
在![]() 内部时,如图②,以点
内部时,如图②,以点![]() 为顶点作
为顶点作![]() ,使
,使![]() 的两边分别和
的两边分别和![]() 的两边垂直,垂足分别为
的两边垂直,垂足分别为![]() 、
、![]() ,用数学式子写出
,用数学式子写出![]() 和
和![]() 的数量关系;
的数量关系;
(3)由上述情形,用文字语言叙述结论:如果一个角的两边分别和另一个角的两边垂直,那么这两个角 .
(4)在图②中,若![]() ,求
,求![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织了“健康教育”手抄报征集活动,现从中抽取部分作品,按A、B、C、D四个等级进行奖励,并根据统计结果绘制了如下两幅不完整统计图.
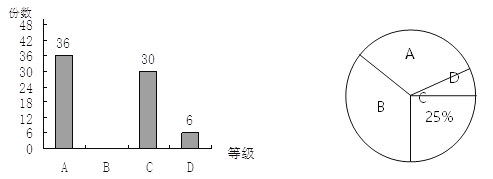
(1)求抽取了多少份作品.
(2)被抽取作品中B等级有多少份?并补全条形统计图.
(3)扇形统计图中D等级所对的圆心角是多少度?
(4)若全校共征集到作品600份,请估计A作品有多少份?
查看答案和解析>>
科目:初中数学 来源: 题型:
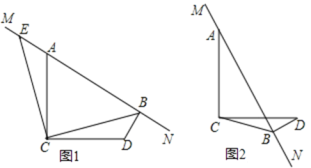
【题目】已知∠ACD=90°,MN是过A点的直线,AC=DC,DB⊥MN于点B,连接BC.
(1)如图1,将△BCD绕点C逆时针方向旋转90°得到△ECA.
①求证:点E在直线MN上;
②猜想线段AB、BD、CB满足怎样的数量关系,并证明你的猜想.
(2)当MN绕点A旋转到如图2的位置时,猜想线段AB、BD、CB又满足怎样的数列关系,并证明你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学附近的文具用品商店最近新进了一批涂卡笔,每支8元,为了合理定价,在第一周试行机动价格,卖出时每支以10元为标准,超出10元的部分记为正,不足10元的部分记为负,文具店售货员记录了第一周涂卡笔的售价情况和售出情况:
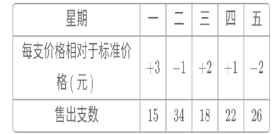
(1)这一周文具用品店的涂卡笔哪天售出的单价最高?最高单价是多少元?
(2)这一周文具用品店出售此种涂卡笔的收益如何?(盈利或亏损的钱数)
(3)文具用品店为了促销这种涂卡笔,决定从下周一起推出两种促销方式:
方式一:购买不超过3支涂卡笔,每支12元,超出3支的部分,每支打九折;
方式二:每支售价12元,购买一支涂卡笔就赠送成本价为0.8元的矿泉水一瓶。
有名同学想一次性购买6支涂卡笔,文具店希望该同学通过哪种方式购买才会使文具店盈利较多?请通过计算说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在平面直角坐标系中,如图,点![]() ,点
,点![]() ,连接
,连接![]() ,过点B作直线
,过点B作直线![]() 交
交![]() 于A点,设直线
于A点,设直线![]() 的解析式为
的解析式为![]()
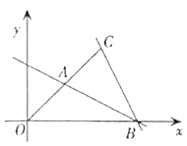
(1)求直线![]() 的函数关系式;
的函数关系式;
(2)若直线![]() 平分
平分![]() 的面积时,求A到x轴的距离;
的面积时,求A到x轴的距离;
(3)作点C关于y轴的对称点D,若直线![]() 与线段
与线段![]() 有交点,求k的取值范围.
有交点,求k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com