
【题目】P为等边△ABC内的一点,PA=10,PB=6,PC=8,将△ABP绕点B顺时针旋转60°到△CBP′位置.
(1)判断△BPP′的形状,并说明理由;
(2)求∠BPC的度数.
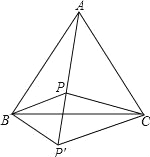
【答案】(1) △BPP′是等边三角形,理由详见解析;(2)150°.
【解析】
试题分析:(1)根据旋转的性质得BP=BP′,∠PBP’=60°,AP=CP′=10,则利用等边三角形的判定方法可判断△BPP′是等边三角形;
(2)利用△BPP′是等边三角形得到∠BPP′=60°,PP′=PB=6,然后利用勾股定理的逆定理可证明△PCP′是直角三角形,∠P′PC=90°,再计算∠BPP′+∠P′PC即可.
试题解析:(1)△BPP′是等边三角形;理由如下:
∵△ABP绕点B顺时针旋转60°到△CBP′位置,
∴BP=BP′,∠PBP′=60°,AP=CP′=10,
∴△BPP′是等边三角形;
(2)∵△BPP′是等边三角形,
∴∠BPP′=60°,PP′=PB=6,
∵![]() ,
,
∴![]() ,
,
∴△PCP′是直角三角形,∠P′PC=90°,
∴∠BPC=∠BPP′+∠P′PC=60°+90°=150°.


科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=![]() 与x轴交于A、B两点.
与x轴交于A、B两点.
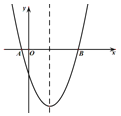
(1)点A的坐标是 ,点B的坐标是 ,抛物线的对称轴是直线 ;
(2)将抛物线向上平移m个单位,与x轴交于C、D两点(点C 在点D的左边).若CD:AB=3:4,求m的值;
(3)点P是(2)中平移后的抛物线上y轴右侧部分的点,直线y=2x+b(b![]() 0)与 x、y轴分别交于点E、F.若以EF为直角边的三角形PEF与△OEF相似,直接写出点P的坐标.
0)与 x、y轴分别交于点E、F.若以EF为直角边的三角形PEF与△OEF相似,直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店为了促销一种定价为26元/千克鸡蛋糕,采取下列方式优惠销售.若一次性购买不超过5千克按原价付款;若一次性购买5千克以上超过部分按原价八折付款,如果小明有338元钱,那么他最多可以购买该鸡蛋糕________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两人进行飞镖比赛,每人各投5次,其中甲所得环数的方差为15,乙所得环数的方差为12.5,那么成绩较稳定的是_______(填“甲”或“乙”).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以下列各组线段为边,能组成三角形的是().
A. 2cm,3cm,5cmB. 5cm,6cm,10cm
C. 1cm,1cm,3cmD. 3cm,4cm,9cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某篮球队在平时训练中,运动员甲的3分球命中率是70%,运动员乙的3分球命中率是50%. 在一场比赛中,甲投3分球4次,命中一次;乙投3分球4次,全部命中. 全场比赛即将结束,甲、乙两人所在球队还落后对方球队2分,但只有最后一次进攻机会了,若你是这个球队的教练,问:(1)最后一个3分球由甲、乙中谁来投,获胜的机会更大?(2)请简要说说你的理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形![]() 的边长
的边长![]() .某一时刻,动点
.某一时刻,动点![]() 从
从![]() 点出发沿
点出发沿![]() 方向以
方向以![]() 的速度向
的速度向![]() 点匀速运动;同时,动点
点匀速运动;同时,动点![]() 从
从![]() 点出发沿
点出发沿![]() 方向以
方向以![]() 的速度向
的速度向![]() 点匀速运动,问:
点匀速运动,问:

(1)经过多少时间,![]() 的面积等于矩形
的面积等于矩形![]() 面积的
面积的![]() ?
?
(2)是否存在时刻t,使以A,M,N为顶点的三角形与![]() 相似?若存在,求t的值;若不存在,请说明理由.
相似?若存在,求t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】密苏里州圣路易斯拱门是座雄伟壮观的抛物线形的建筑物,是美国最高的独自挺立的纪念碑,如图.拱门的地面宽度为200米,两侧距地面高150米处各有一个观光窗,两窗的水平距离为100米,求拱门的最大高度.
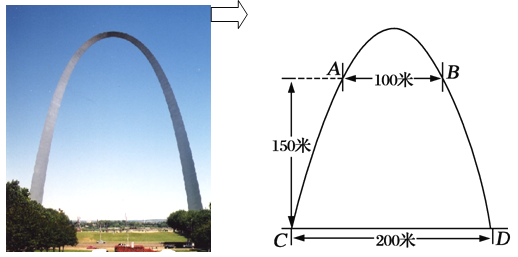
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=3x2+2x-1向上平移4个单位长度后的函数解析式为( )
A. y=3x2+2x-5 B. y=3x2+2x-4 C. y=3x2+2x+3 D. y=3x2+2x+4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com