
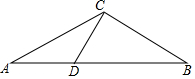
 如图,在△ABC中,∠A=30°,D为边AB上的点,且DA=DC=2,若△DCB绕点D逆时针旋转,使DB、DC分别与线段AC相交于M、N,则当△DMN为等边三角形时,DM的长值为$\frac{2\sqrt{3}}{3}$.
如图,在△ABC中,∠A=30°,D为边AB上的点,且DA=DC=2,若△DCB绕点D逆时针旋转,使DB、DC分别与线段AC相交于M、N,则当△DMN为等边三角形时,DM的长值为$\frac{2\sqrt{3}}{3}$. 分析 作出图形,过点D作DE⊥AC于E,根据直角三角形30°角所对的直角边等于斜边的一半可得DE=$\frac{1}{2}$AD,再根据等边三角形的性质求解即可.
解答 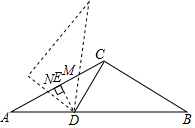 解:如图,过点D作DE⊥AC于E,
解:如图,过点D作DE⊥AC于E,
∵∠A=30°,DA=DC=2,
∴DE=$\frac{1}{2}$AD=$\frac{1}{2}$×2=1,
∵△DMN为等边三角形,
∴DM=DE÷$\frac{\sqrt{3}}{2}$=1÷$\frac{\sqrt{3}}{2}$=$\frac{2\sqrt{3}}{3}$.
故答案为:$\frac{2\sqrt{3}}{3}$.
点评 本题考查了旋转的性质,主要利用了直角三角形30°角所对的直角边等于斜边的一半以及等边三角形的性质,作辅助线构造出直角三角形是解题的关键.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 经销商小李需要购进一批学生画图工具6000套,为此考察了甲、乙两个文具加工厂.已知甲厂的加工能力是乙厂的1.5倍,且甲厂单独加工这批画图工具所需要的天数比乙厂单独加工这批画图工具所需要的天数少10天,还了解到这种画图工具:甲厂的出厂价格为6元/套,乙厂的出厂价格为5.6元/套.
经销商小李需要购进一批学生画图工具6000套,为此考察了甲、乙两个文具加工厂.已知甲厂的加工能力是乙厂的1.5倍,且甲厂单独加工这批画图工具所需要的天数比乙厂单独加工这批画图工具所需要的天数少10天,还了解到这种画图工具:甲厂的出厂价格为6元/套,乙厂的出厂价格为5.6元/套.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 乘坐高铁对旅客的行李的检查 | |
| B. | 了解福建省2017届初三毕业班家长对省中考统考的意见 | |
| C. | 调查小明所在班级的学生使用手机情况 | |
| D. | 对新研发的新型战斗机的零部件进行检查 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
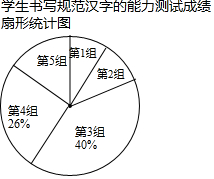 某校为了调查学生书写汉字的能力,从七年级1000名学生中随机抽选了部分学生参加测试,并根据测试成绩绘制出如下频数分布表和扇形统计图:
某校为了调查学生书写汉字的能力,从七年级1000名学生中随机抽选了部分学生参加测试,并根据测试成绩绘制出如下频数分布表和扇形统计图:| 组别 | 成绩x分 | 频数(人数) |
| 第1组 | x<60 | 4 |
| 第2组 | 60≤x<70 | a |
| 第3组 | 70≤x<80 | 20 |
| 第4组 | 80≤x<90 | b |
| 第5组 | 90≤x≤100 | 10 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com