
【题目】如图,在平面直角坐标系中,抛物线![]() 与x轴交于B、C两点(点B在点C的左侧),与y轴交于点A,抛物线的顶点为D.
与x轴交于B、C两点(点B在点C的左侧),与y轴交于点A,抛物线的顶点为D.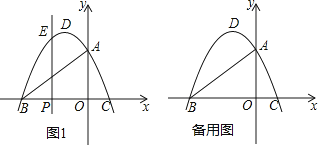
(1)填空:点A的坐标为( , ),点B的坐标为( , ),点C的坐标为( , ),点D的坐标为( , );
(2)点P是线段BC上的动点(点P不与点B、C重合)
①过点P作x轴的垂线交抛物线于点E,若PE=PC,求点E的坐标;
②在①的条件下,点F是坐标轴上的点,且点F到EA和ED的距离相等,请直接写出线段EF的长;
③若点Q是线段AB上的动点(点Q不与点A、B重合),点R是线段AC上的动点(点R不与点A、C重合),请直接写出△PQR周长的最小值.
【答案】
(1)
解:令x=0,则y=2,
∴A(0,2),
令y=0,则﹣![]() x2﹣
x2﹣![]() x+2=0,解得x1=﹣3,x2=1(舍去),
x+2=0,解得x1=﹣3,x2=1(舍去),
∴B(﹣3,0),C(1,0),
由y=﹣![]() x2﹣
x2﹣![]() x+2=﹣
x+2=﹣![]() (x+1)2+
(x+1)2+![]() 可知D(﹣1,
可知D(﹣1,![]() ),
),
故答案为:0、2,﹣3、0,1、0,﹣1、![]() ;
;
(2)
解:①设P(n,0),则E(n,﹣![]() n2﹣
n2﹣![]() n+2),
n+2),
∵PE=PC,
∴﹣![]() n2﹣
n2﹣![]() n+2=1﹣n,解得n1=﹣
n+2=1﹣n,解得n1=﹣![]() ,n2=1(舍去),
,n2=1(舍去),
∴当n=﹣![]() 时,1﹣n=
时,1﹣n=![]() ,
,
∴E(﹣![]() ,
,![]() ),
),
②如图1,设直线DE与x轴交于M,与y轴交于N,直线EA与x轴交于K,
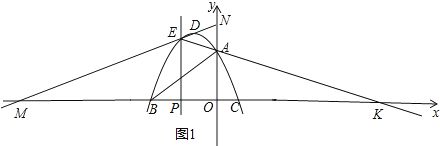
根据E、D的坐标求得直线ED的斜率为![]() ,根据E、A的坐标求得直线EA的斜率为﹣
,根据E、A的坐标求得直线EA的斜率为﹣![]() ,
,
∴△MEK是以MK为底边的等腰三角形,△AEN是以AN为底边的等腰三角形,
∵到EA和ED的距离相等的点F在顶角的平分线上,
根据等腰三角形的性质可知,EF是E点到坐标轴的距离,
∴EF=![]() 或
或![]() ;
;
③根据题意得:当△PQR为△ABC垂足三角形时,周长最小,所以P与O重合时,周长最小,
如图2,作O关于AB的对称点E,作O关于AC的对称点F,连接EF交AB于Q,交AC于R,
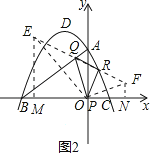
此时△PQR的周长PQ+QR+PR=EF,
∵A(0,2),B(﹣3,0),C(1,0),
∴AB=![]() =
=![]() ,AC=
,AC=![]() =
=![]() ,
,
∵S△AOB=![]() ×
×![]() OE×AB=
OE×AB=![]() OAOB,
OAOB,
∴OE=![]() ,
,
∵△OEM∽△ABO,
∴![]() =
=![]() =
=![]() ,即
,即![]() =
=![]() =
=![]() ,
,
∴OM=![]() ,EM=
,EM=![]()
∴E(﹣![]() ,
,![]() ),
),
同理求得F(![]() ,
,![]() ),
),
即△PQR周长的最小值为EF=![]() =
=![]() .
.
【解析】(1)令x=0,求得A(0,2),令y=0,求得B(﹣3,0),C(1,0),由y=﹣![]() x2﹣
x2﹣![]() x+2转化成顶点式可知D(﹣1,
x+2转化成顶点式可知D(﹣1,![]() );
);
(2)①设P(n,0),则E(n,﹣![]() n2﹣
n2﹣![]() n+2),根据已知条件得出﹣
n+2),根据已知条件得出﹣![]() n2﹣
n2﹣![]() n+2=1﹣n,解方程即可求得E的坐标;
n+2=1﹣n,解方程即可求得E的坐标;
②根据直线ED和EA的斜率可知直线与坐标轴的交角相等,从而求得与坐标轴构成的三角形是等腰三角形,根据等腰三角形的性质即可求得EF的长;
③根据题意得:当△PQR为△ABC垂足三角形时,周长最小,所以P与O重合时,周长最小,作O关于AB的对称点E,作O关于AC的对称点F,连接EF交AB于Q,交AC于R,此时△PQR的周长PQ+QR+PR=EF,然后求得E、F的坐标,根据勾股定理即可求得.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:
【题目】如图,分别以直角△ABC的斜边AB,直角边AC为边向△ABC外作等边△ABD和等边△ACE,F为AB的中点,DE与AB交于点G,EF与AC交于点H,∠ACB=90°,∠BAC=30°.给出如下结论:
①EF⊥AC;②四边形ADFE为菱形;③AD=4AG;④FH= ![]() BD
BD
其中正确结论的为(请将所有正确的序号都填上).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】雾霾天气严重影响市民的生活质量.在今年寒假期间,某校八年级一班的综合实践小组同学对“雾霾天气的主要成因”随机调查了所在城市部分市民.并对调查结果进行了整理.绘制了如图不完整的统计图表.观察分析并回答下列问题.![]()
(1)本次被调查的市民共有多少人?
(2)分别补全条形统计图和扇形统计图,并计算图2中区域B所对应的扇形圆心角的度数;
(3)若该市有100万人口,请估计持有A、B两组主要成因的市民有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某蔬菜经销商去蔬菜生产基地批发某种蔬菜,已知这种蔬菜的批发量在20千克~60千克之间(含20千克和60千克)时,每千克批发价是5元;若超过60千克时,批发的这种蔬菜全部打八折,但批发总金额不得少于300元.
(1)根据题意,填写下表:
蔬菜的批发量(千克) | … | 25 | 60 | 75 | 90 | … |
所付的金额(元) | … | 125 |
| 300 |
| … |
(2)经调查,该蔬菜经销商销售该种蔬菜的日销售量y(千克)与零售价x(元/千克)是一次函数关系,其图象如图,求出y与x之间的函数关系式;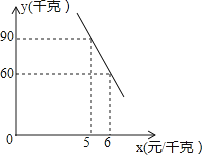
(3)若该蔬菜经销商每日销售此种蔬菜不低于75千克,且当日零售价不变,那么零售价定为多少时,该经销商销售此种蔬菜的当日利润最大?最大利润为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】高速铁路列车已成为中国人出行的重要交通工具,其平均速度是普通铁路列车平均速度的3倍,同样行驶690km,高速铁路列车比普通铁路列车少运行了4.6h,求高速铁路列车的平均速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的边长为2,∠DAB=60°,E为BC的中点,在对角线AC上存在一点P,使△PBE的周长最小,则△PBE的周长的最小值为 . 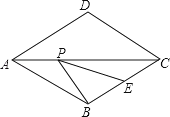
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,AB为⊙O的直径,点P是直径AB上任意一点,过点P作弦CD⊥AB,垂足为P,过点B的直线与线段AD的延长线交于点F,且∠F=∠ABC.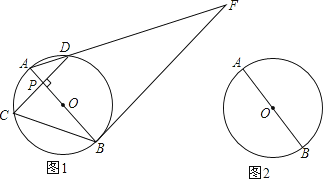
(1)若CD=![]() ,BP=4,求⊙O的半径;
,BP=4,求⊙O的半径;
(2)求证:直线BF是⊙O的切线;
(3)当点P与点O重合时,过点A作⊙O的切线交线段BC的延长线于点E,在其它条件不变的情况下,判断四边形AEBF是什么特殊的四边形?请在图2中补全图象并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,Rt△OA1C1 , Rt△OA2C2 , Rt△OA3C3 , Rt△OA4C4…的斜边都在坐标轴上,∠A1OC1=∠A2OC2=∠A3OC3=∠A4OC4…=30°.若点A1的坐标为(3,0),OA1=OC2 , OA2=OC3 , OA3=OC4…,则依次规律,点A2016的纵坐标为( )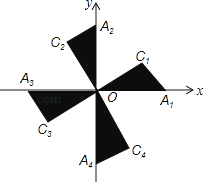
A.0
B.﹣3×( ![]() )2015
)2015
C.(2 ![]() )2016
)2016
D.3×( ![]() )2015
)2015
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD的对角线AC、BD相交于点O,EF、GH过点O,且点E、H在边AB上,点G、F在边CD上,向ABCD内部投掷飞镖(每次均落在ABCD内,且落在ABCD内任何一点的机会均等)恰好落在阴影区域的概率为( )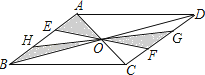
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com