
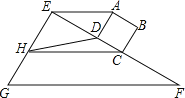
【题目】如图,正方形ABCD的边CD与Rt△EFG的直角边EF重合,将正方形ABCD以1cm/s的速度沿FE方向移动,在移动过程中,边CD始终与边EF重合(移动开始时点C与点F重合).连接AE,过点C作AE的平行线交直线EG于点H,连接HD.已知正方形ABCD的边长为1cm,EF=4cm,设正方形移动时间为x(s),线段EH的长为y(cm),其中0≤x≤2.5.
(1)当x=2时,AE的长为 ;
(2)试求出y关于x的函数关系式,并求出△EHD与△ADE的面积之差;
(3)当正方形ABCD移动时间x= 时,线段HD所在直线经过点B.
【答案】(1)![]() cm(2)
cm(2)![]() ;(3)
;(3)![]()
【解析】
试题分析:(1)根据正方形的性质得到∠ADE=90°,根据勾股定理计算即可;
(2)根据题意表示出EC=4﹣x,ED=3﹣x,证明△AED∽△HCE,根据相似三角形的性质得到比例式,代入计算即可;
(3)根据正方形的性质得到∠ADB=45°,根据等腰直角三角形的性质列出方程,解方程即可.
解:(1)当x=2时,即CF=2cm,
则EC=EF﹣CF=2cm,又CD=1cm,
∴ED=1cm,
∵四边形ABCD是正方形,
∴∠ADE=90°,
∴AE=![]() =
=![]() cm,
cm,
故答案为:![]() cm;
cm;
(2)∵正方形移动时间为x(s),
∴CF=x,
则EC=4﹣x,ED=3﹣x,
∵AE∥HC,
∴∠AED=∠HCE,又∠ADE=∠HEC,
∴△AED∽△HCE,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得,y=![]() ,
,
△ADE的面积=![]() ×(3﹣x)×1=
×(3﹣x)×1=![]() ,
,
△EHC的面积=![]() ×(4﹣x)×
×(4﹣x)×![]() =
=![]() ,
,
则△EHD的面积=![]() ×
×![]() ×
×![]() =
=![]() ,
,
△EHD的面积﹣△ADE的面积=![]() ;
;
(3)当线段HD所在直线经过点B时,
∵∠ADB=45°,∠ADE=90°,
∴∠EDH=45°,
∴EH=ED,即![]() =3﹣x,
=3﹣x,
解得,x1=![]() ,x2=
,x2=![]() (舍去),
(舍去),
故答案为:![]() .
.


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案科目:初中数学 来源: 题型:
【题目】已知△ABC中,a、b、c分别为∠A、∠B、∠C的对边,方程cx2+bx﹣a=0是关于x的一元二次方程.

(1)判断方程cx2+bx﹣a=0的根的情况为 (填序号);
①方程有两个相等的实数根;
②方程有两个不相等的实数根;
③方程无实数根;
④无法判断
(2)如图,若△ABC内接于半径为2的⊙O,直径BD⊥AC于点E,且∠D=30°,求方程cx2+bx﹣a=0的根;
(3)若x=![]() a是方程cx2+bx﹣a=0的一个根,△ABC的三边a、b、c的长均为整数,试求a、b、c的值.
a是方程cx2+bx﹣a=0的一个根,△ABC的三边a、b、c的长均为整数,试求a、b、c的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以下是某校九年级10名同学参加学校演讲比赛的统计表:
成绩/分 | 80 | 85 | 90 | 95 |
人数/人 | 1 | 2 | 5 | 2 |
则这组数据的中位数和平均数分别为( )
A. 90,90 B. 90,89 C. 85,89 D. 85,90
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】足球比赛的记分为:胜一场得3分,平一场得1分,负一场得0分,一队打了14场比赛,负5场,共得19分,那么这个队胜了( )
A. 3场 B. 4场 C. 5场 D. 6场
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】美国航空航天局发布消息,2011年3月19日,月球将到达19年来距离地球最近的位置,它与地球的距离约为356000千米,其中356000用科学记数法表示为 ( )
A. 3.56×105 B. 0.356×106 C. 3.56×104 D. 35.6×104
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com