
【题目】已知:在![]() 中,
中,![]() ,
,![]() 都是
都是![]() 的半径,过
的半径,过![]() 作
作![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 的切线交
的切线交![]() 的延长线于点
的延长线于点![]() .
.
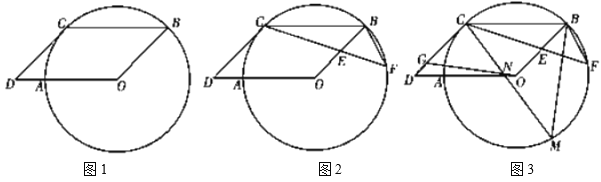
(1)如图1,求证:![]() ;
;
(2)如图2,点![]() 在
在![]() 上,连接
上,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,连接
,连接![]() ,若
,若![]() ,求证:四边形
,求证:四边形![]() 是平行四边形;
是平行四边形;
(3)如图3,在(2)的条件下,点![]() 在
在![]() 上,连接
上,连接![]() ,且
,且![]() ,点
,点![]() 在
在![]() 上,连接
上,连接![]() ,
,![]() ,
,![]() 交
交![]() 于点
于点![]() ,且
,且![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的长.
的长.
【答案】(1)见解析;(2)见解析;(3)32
【解析】
(1)连接OC,根据切线性质得到![]() ,根据等腰三角形的性质得到
,根据等腰三角形的性质得到![]() ,再根据平行线的性质,即可得出结论; (2)根据同弧所对的圆心角是圆周角的两倍,算出
,再根据平行线的性质,即可得出结论; (2)根据同弧所对的圆心角是圆周角的两倍,算出![]() 的度数,得出
的度数,得出![]() ,从而判断出是平行四边形;(3)连接OC,作
,从而判断出是平行四边形;(3)连接OC,作![]() 的平分线交DC的延长线于点P,延长GO交BM于Q,设
的平分线交DC的延长线于点P,延长GO交BM于Q,设![]() 证明
证明![]() ,得到
,得到![]() ,根据勾股定理列式求出
,根据勾股定理列式求出![]() ,根据正弦的定义、垂径定理计算,得出答案.
,根据正弦的定义、垂径定理计算,得出答案.
(l)证明:如图1连接![]()
![]()
![]()
![]()
![]()
![]()
![]() 切
切![]() 于点
于点![]()
![]()
![]()
![]()
![]()
图1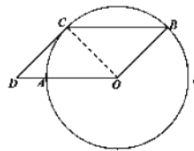
(2)证明:如图2连接![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]() 四边形
四边形![]() 是平行四边形.
是平行四边形.
图2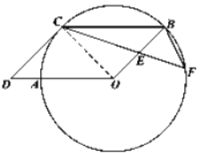
(3)解:如图3连接![]() ,作
,作![]() 平分交
平分交![]() 的延长线于点
的延长线于点![]() ,延长
,延长![]() 交
交![]() 于点
于点![]()
令![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,![]()
![]() 四边形
四边形![]() 是平行四边形
是平行四边形
![]() ,
,![]()
![]()
![]()
![]() ,
,![]() ,
,![]()
又![]()
![]()
![]()
![]()
![]()
在![]() 中,
中,![]()
![]()
解得![]() ,
,![]() (舍)
(舍)
![]() ,
,![]() .
.
![]()
![]()
![]()
![]()
![]()
![]()
在![]() 中,
中,![]()
在![]() 中,
中,![]()
![]()
![]()
![]()
![]() .
.
图3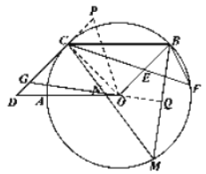


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】某企业接到一批防护服生产任务,按要求15天完成,已知这批防护服的出厂价为每件80元,为按时完成任务,该企业动员放假回家的工人及时返回加班赶制.该企业第![]() 天生产的防护服数量为
天生产的防护服数量为![]() 件,
件,![]() 与
与![]() 之间的关系可以用图中的函数图象来刻画.
之间的关系可以用图中的函数图象来刻画.

(1)直接写出![]() 与
与![]() 的函数关系式________;
的函数关系式________;
(2)由于疫情加重,原材料紧缺,防护服的成本前5天为每件50元,从第6天起每件防护服的成本比前一天增加2元,设第![]() 天创造的利润为
天创造的利润为![]() 元,直接利用(1)的结论,求
元,直接利用(1)的结论,求![]() 与
与![]() 之间的函数表达式,并求出第几天的利润最大,最大利润是多少元?(利润=出厂价-成本)
之间的函数表达式,并求出第几天的利润最大,最大利润是多少元?(利润=出厂价-成本)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某社区购买甲、乙两种树苗进行绿化,购买一棵甲种树苗的价钱比购买一棵乙种树苗的价钱多 10 元钱,已知购买 20 棵甲种树苗、30 棵乙种树苗共需 1 200 元钱.
(1)求购买一棵甲种、一棵乙种树苗各多少元?
(2)社区决定购买甲、乙两种树苗共 400 棵,总费用不超过 10 600 元,那么该社区最多可以购买多少棵甲种树苗?
查看答案和解析>>
科目:初中数学 来源: 题型:
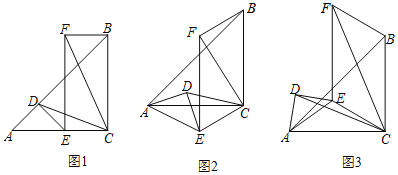
【题目】已知△ACB和△ADE都是等腰直角三角形,∠ACB=∠ADE=90°,以CE、BC为边作平行四边形CEFB,连CD、CF.
(1)如图1,当E、D分别在AC和AB上时,求证:CD=![]() CF;
CF;
(2)如图2,△ADE绕点A旋转一定角度,判断(1)中CD与CF的数量关系是否依然成立,并加以证明;
(3)如图3,AE=![]() ,AB=
,AB=![]() ,将△ADE绕A点旋转一周,当四边形CEFB为菱形时,直接写出CF的长.
,将△ADE绕A点旋转一周,当四边形CEFB为菱形时,直接写出CF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践 在![]() 中,
中,![]() ,点
,点![]() 为斜边
为斜边![]() 上的动点(不与点
上的动点(不与点![]() 重合).
重合).
(1)操作发现: 如图①,当![]() 时,把线段
时,把线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到线段
得到线段![]() ,连接
,连接![]() .
.
①![]() 的度数为________;
的度数为________;
②当![]() ________时,四边形
________时,四边形![]() 为正方形;
为正方形;

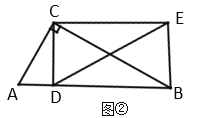
(2)探究证明: 如图②,当![]() 时,把线段
时,把线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 后并延长为原来的两倍, 记为线段
后并延长为原来的两倍, 记为线段![]() ,连接
,连接![]() .
.
①在点![]() 的运动过程中,请判断
的运动过程中,请判断![]() 与
与![]() 的大小关系,并证明;
的大小关系,并证明;
②当 时,求证:四边形
时,求证:四边形![]() 为矩形.
为矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
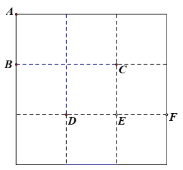
【题目】如图,在3![]() 3的正方形网格中,点A、B、C、D、E、F都是格点.
3的正方形网格中,点A、B、C、D、E、F都是格点.
(1)从A、D、E、F四点中任意取一点,以所取点及B、C为顶点画三角形,那么所画三角形是等腰三角形的概率是 .
(2)从A、D、E、F四点中任意取两点,以所取两点及B、C为顶点画四边形,求所画四边形是平行四边形的概率.(请用“画树状图”或“列表”等方式写出分析过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
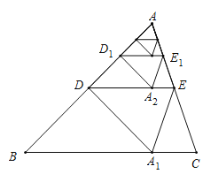
【题目】如图,将![]() 沿着过
沿着过![]() 中点
中点![]() 的直线折叠,使点
的直线折叠,使点![]() 落在
落在![]() 边上的
边上的![]() ,称为第
,称为第![]() 次操作,折痕
次操作,折痕![]() 到
到![]() 的距离记为
的距离记为![]() ;还原纸片后,再将
;还原纸片后,再将![]() 沿着过
沿着过![]() 中点
中点![]() 的直线折叠,使点
的直线折叠,使点![]() 落在
落在![]() 边上的
边上的![]() 处,称为第
处,称为第![]() 次操作,折痕
次操作,折痕![]() 到
到![]() 的距离记为
的距离记为![]() ;按上述方法不断操作下去…,经过第
;按上述方法不断操作下去…,经过第![]() 次操作后得到的折痕
次操作后得到的折痕![]() ,到
,到![]() 的距离记为
的距离记为![]() ,若
,若![]() ,则
,则![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某中学学生课余生活情况,对喜爱看课外书、体育活动、看电视、社会实践四个方面的人数进行调查统计,现从该校随机抽取n名学生作为样本,采用问卷调查的方式收集数据![]() 参与问卷调查的每名学生只能选择其中一项
参与问卷调查的每名学生只能选择其中一项![]() ,并根据调查得到的数据绘制成了如图所示的两幅不完整的统计图,由图中提供的信息,解答下列问题:
,并根据调查得到的数据绘制成了如图所示的两幅不完整的统计图,由图中提供的信息,解答下列问题:

![]() 补全条形统计图;
补全条形统计图;
![]() 若该校共有学生2400名,试估计该校喜爱看电视的学生人数.
若该校共有学生2400名,试估计该校喜爱看电视的学生人数.
![]() 若调查到喜爱体育活动的4名学生中有3名男生和1名女生,现从这4名学生中任意抽取2名,求恰好抽到2名男生的概率.
若调查到喜爱体育活动的4名学生中有3名男生和1名女生,现从这4名学生中任意抽取2名,求恰好抽到2名男生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com