
【题目】根据问题填空:
(1)计算:|﹣3|+tan60°+ ![]() ;
;
(2)化简:(x﹣1)2+x(x+1).
【答案】
(1)解:原式=3+ ![]() +1=4+
+1=4+ ![]() ;
;
(2)解:原式=x2﹣2x+1+x2+x=2x2﹣x+1
【解析】(1)原式利用绝对值的代数意义,零指数幂法则,以及特殊角的三角函数值计算即可得到结果;(2)原式利用完全平方公式,以及单项式乘以多项式法则计算即可得到结果.
【考点精析】认真审题,首先需要了解零指数幂法则(零次幂和负整数指数幂的意义: a0=1(a≠0);a-p=1/ap(a≠0,p为正整数)),还要掌握特殊角的三角函数值(分母口诀:30度、45度、60度的正弦值、余弦值的分母都是2,30度、45度、60度的正切值、余切值的分母都是3,分子口诀:“123,321,三九二十七”)的相关知识才是答题的关键.


科目:初中数学 来源: 题型:
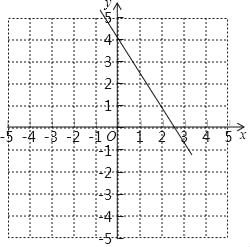
【题目】点A(0,4),B(2,1)是直角坐标系中的两个点.
(1)请在平面直角坐标系中描出A,B两点,并画出直线AB;
(2)写出B点关于y轴的对称点B′的坐标 ;
(3)求出直线AB与x轴的交点坐标 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图所示的方式放置.点A1,A2,A3,…和点C1,C2,C3,…分别在直线y=kx+b(k>0)和x轴上,已知点B1(1,1),B2(3,2),则点B3的坐标是_____;点B2018的坐标是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一块塑料矩形模板ABCD,长为10cm,宽为4cm,将你手中足够大的直角三角板 PHF 的直角顶点P落在AD边上(不与A、D重合),在AD上适当移动三角板顶点P:
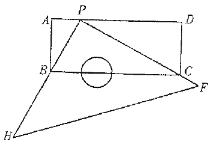
①能否使你的三角板两直角边分别通过点B与点C?若能,请你求出这时 AP 的长;若不能,请说明理由;
②再次移动三角板位置,使三角板顶点P在AD上移动,直角边PH 始终通过点B,另一直角边PF与DC的延长线交于点Q,与BC交于点E,能否使CE=2cm?若能,请你求出这时AP的长;若不能,请你说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
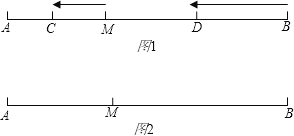
【题目】已知:如图1,M是定长线段AB上一定点,C、D两点分别从M、B出发以1cm/s、3cm/s的速度沿直线BA向左运动,运动方向如箭头所示(C在线段AM上,D在线段BM上)
(1)若AB=10cm,当点C、D运动了2s,求AC+MD的值.
(2)若点C、D运动时,总有MD=3AC,直接填空:AM= AB.
(3)在(2)的条件下,N是直线AB上一点,且AN-BN=MN,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“五一”期间,小明一家乘坐高铁前往某市旅游,计划第二天租用新能源汽车自驾出游。
 [来
[来
根据以上信息,解答下列问题:
(1)设租车时间为![]() 小时,租用甲公司的车所需费用为
小时,租用甲公司的车所需费用为![]() 元,租用乙公司的车所需费用为
元,租用乙公司的车所需费用为![]() 元,分别求出
元,分别求出![]() ,
,![]() 关于
关于![]() 的函数表达式;
的函数表达式;
(2)请你帮助小明计算并选择哪个出游方案合算。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读:对于函数y=ax2+bx+c(a≠0),当t1≤x≤t2时,求y的最值时,主要取决于对称轴x=﹣ ![]() 是否在t1≤x≤t2的范围和a的正负:①当对称轴x=﹣
是否在t1≤x≤t2的范围和a的正负:①当对称轴x=﹣ ![]() 在t1≤x≤t2之内且a>0时,则x=﹣
在t1≤x≤t2之内且a>0时,则x=﹣ ![]() 时y有最小值,x=t1或x=t2时y有最大值;②当对称轴x=﹣
时y有最小值,x=t1或x=t2时y有最大值;②当对称轴x=﹣ ![]() 在t1≤x≤t2之内且a<0时,则x=﹣
在t1≤x≤t2之内且a<0时,则x=﹣ ![]() 时y有最大值,x=t1或x=t2时y有最小值;③当对称轴x=﹣
时y有最大值,x=t1或x=t2时y有最小值;③当对称轴x=﹣ ![]() 不在t1≤x≤t2之内,则函数在x=t1或x=t2时y有最值.
不在t1≤x≤t2之内,则函数在x=t1或x=t2时y有最值.
解决问题:
设二次函数y1=a(x﹣2)2+c(a≠0)的图象与y轴的交点为(0,1),且2a+c=0.
(1)求a、c的值;
(2)当﹣2≤x≤1时,直接写出函数的最大值和最小值;
(3)对于任意实数k,规定:当﹣2≤x≤1时,关于x的函数y2=y1﹣kx的最小值称为k的“特别值”,记作g(k),求g(k)的解析式;
(4)在(3)的条件下,当“特别值”g(k)=1时,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() ,
,![]() ,
,![]() .
.


备用图
(1)直接写出![]() _________;
_________;
(2)已知点![]() ,满足
,满足![]() ,求
,求![]() 的值;
的值;
(3)如图,把直线![]() 以每秒
以每秒![]() 个单位长度的速度向右平移,求平移多少秒时该直线恰好经过
个单位长度的速度向右平移,求平移多少秒时该直线恰好经过![]() 点.
点.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com