
ЁОЬтФПЁПФГЮвЪаЛЈЪЏеђзщжЏ10СОЦћГЕзАдЫЭъAЁЂBЁЂCШ§жжВЛЭЌЦЗжЪЕФЯцСЋЙВ100ЖжЕНЭтЕиЯњЪлЃЌАДМЦЛЎ10СОЦћГЕЖМвЊзАТњЃЌЧвУПСОЦћГЕжЛФмзАЭЌвЛжжЯцСЋЃЌИљОнЯТБэЬсЙЉЕФаХЯЂЃЌНтД№вдЯТЮЪЬтЃК
ЃЈ1ЃЉЩшзАдЫAжжЯцСЋЕФГЕСОЪ§ЮЊxЃЌзАдЫBжжЯцСЋЕФГЕСОЪ§ЮЊyЃЌЧѓyгыxжЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ2ЃЉШчЙћзАдЫУПжжЯцСЋЕФГЕСОЪ§ЖМВЛЩйгк2СОЃЌФЧУДГЕСОЕФАВХХЗНАИгаМИжжЃПВЂаДГіУПжжАВХХЗНАИЃЛ
ЃЈ3ЃЉШєвЊЪЙДЫДЮЯњЪлЛёРћзюДѓЃЌгІВЩгУФФжжАВХХЗНАИЃПВЂЧѓГізюДѓРћШѓЕФжЕЃЎ
ЯцСЋЦЗжж | A | B | C |
УПСОЦћГЕдЫдиСП(Жж) | 12 | 10 | 8 |
УПЖжЯцСЋЛёРћ(ЭђдЊ) | 3 | 4 | 2 |
ЁОД№АИЁПЃЈ1ЃЉy=10Љ2xЃЛЃЈ2ЃЉга3жжАВХХЗНАИЃКЗНАИвЛЃКзАAжж2СОГЕЃЌзАBжж6СОГЕЃЌзАCжж2СОГЕЃЛЗНАИЖўЃКзАAжж3СОГЕЃЌзАBжж4СОГЕЃЌзАCжж3СОГЕЃЛЗНАИШ§ЃКзАAжж4СОГЕЃЌзАBжж2СОГЕЃЌзАCжж4СОГЕЃЛЃЈ3ЃЉзАAжж2СОГЕЃЌзАBжж6СОГЕЃЌзАCжж2СОГЕЃЌзюДѓРћШѓЮЊ344ЭђдЊЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЬтвтСаЪНЃК12x+10y+8ЃЈ10-x-yЃЉ=100ЃЌБфаЮКѓМДПЩЕУЕНy=10Љ2xЃЛ
ЃЈ2ЃЉИљОнзАдЫУПжжЫЎЙћЕФГЕСОЪ§ЖМВЛЩйгк2СОЃЌxЁн2ЃЌyЁн2ЃЌНтВЛЕШЪНзщМДПЩЃЛ
ЃЈ3ЃЉНсКЯЬтвтЃЌЩшзюДѓРћШѓЮЊWЃЈЭђдЊЃЉЃЌвРЬтвтПЩСаГіБэЪОЪНЃЌW=-28x+400ЃЌПЩжЊКЏЪ§ЮЊМѕКЏЪ§ЃЌМДПЩЕУГіЕБx=2ЪБЃЌWзюДѓЃЎ
НтЃКЃЈ1ЃЉЩшзАAжжЮЊxСОЃЌзАBжжЮЊyСОЃЌдђзАCжжЮЊ10ЉxЉyСОЃЌ
гЩЬтвтЕУЃК12x+10y+8ЃЈ10ЉxЉyЃЉ=100ЃЌ
Ёрy=10Љ2xЃЛ
ЃЈ2ЃЉ10-x-y=10-x-ЃЈ10-2xЃЉ=xЃЌ
ЙЪзАCжжЯцСЋЕФГЕвВЮЊ x СОЃЌ
Ёр![]()
НтЕУЃК2ЁмxЁм4ЃЎxЮЊећЪ§ЃЌ
Ёрx=2ЃЌ3ЃЌ4ЃЌ
ЙЪГЕСОга3жжАВХХЗНАИЃЌЗНАИШчЯТЃК
ЗНАИвЛЃКзАAжж2СОГЕЃЌзАBжж6СОГЕЃЌзАCжж2СОГЕЃЛ
ЗНАИЖўЃКзАAжж3СОГЕЃЌзАBжж4СОГЕЃЌзАCжж3СОГЕЃЛ
ЗНАИШ§ЃКзАAжж4СОГЕЃЌзАBжж2СОГЕЃЌзАCжж4СОГЕЃЛ
ЃЈ3ЃЉЩшЯњЪлРћШѓЮЊWЃЈЭђдЊЃЉЃЌдђ
W=3ЁС12x+4ЁС10ЁСЃЈ10Љ2xЃЉ+2ЁС8x=Љ28x+400ЃЌ
ЁрWЪЧxЕФвЛДЮКЏЪ§ЃЌЧвxдіДѓЪБЃЌWМѕЩйЃЌ
Ёрx=2ЪБЃЌМДЗНАИЮЊЃКзАAжж2СОГЕЃЌзАBжж6СОГЕЃЌзАCжж2СОГЕЃЌ
РћШѓWзюДѓ=400Љ28ЁС2=344ЃЈЭђдЊЃЉЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊAЁЂBСНЕуЕФзјБъЗжБ№ЮЊЃЈЈD2ЃЌ0ЃЉ,ЃЈ0ЃЌ1ЃЉЃЌЁбCЕФдВаФзјБъЮЊЃЈ0ЃЌЈD1ЃЉЃЌАыОЖЮЊ1ЃЎШєDЪЧЁбCЩЯЕФвЛИіЖЏЕуЃЌЩфЯпADгыyжсНЛгкЕуEЃЌдђЁїABEУцЛ§ЕФзюДѓжЕЪЧ( ) 
A. 4 B. ![]() C.
C. ![]() D. 3
D. 3
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
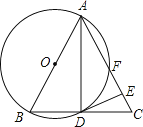
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌAB=ACЃЌвдABЮЊжБОЖЕФЁбOгыBCНЛгкЕуDЃЌгыACНЛгкЕуFЃЌЙ§ЕуDзїЁбOЕФЧаЯпНЛACгкEЃЎ
ЃЈ1ЃЉЧѓжЄЃКAD2=ABAEЃЛ
ЃЈ2ЃЉШєAD=2![]() ЃЌAF=3ЃЌЧѓЁбOЕФАыОЖЃЎ
ЃЌAF=3ЃЌЧѓЁбOЕФАыОЖЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌвбжЊЁїABCЕФШ§ИіЖЅЕуЕФзјБъЗжБ№ЮЊAЃЈЉ5ЃЌ1ЃЉЃЌBЃЈЉ2ЃЌ2ЃЉЃЌCЃЈЉ1ЃЌ4ЃЉЃЌЧыАДЯТСавЊЧѓЛЭМЃК
ЃЈ1ЃЉНЋЁїABCЯШЯђгвЦНвЦ4ИіЕЅЮЛГЄЖШЁЂдйЯђЯТЦНвЦ1ИіЕЅЮЛГЄЖШЃЌЕУЕНЁїA1B1C1ЃЌЛГіЁїA1B1C1ЃЛ
ЃЈ2ЃЉЛГігыЁїABCЙигкдЕуOГЩжааФЖдГЦЕФЁїA2B2C2ЃЌВЂжБНгаДГіЕуA2ЕФзјБъЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊжБЯпl1ЃКy=![]() x-3гыxжсЃЌyжсЗжБ№НЛгкЕуAКЭЕуBЃЎ
x-3гыxжсЃЌyжсЗжБ№НЛгкЕуAКЭЕуBЃЎ
ЃЈ1ЃЉЧѓЕуAКЭЕуBЕФзјБъЃЛ
ЃЈ2ЃЉНЋжБЯпl1ЯђЩЯЦНвЦ6ИіЕЅЮЛКѓЕУЕНжБЯпl2ЃЌЧѓжБЯпl2ЕФКЏЪ§НтЮіЪНЃЛ
ЃЈ3ЃЉЩшжБЯпl2гыxжсЕФНЛЕуЮЊMЃЌдђЁїMABЕФУцЛ§ЪЧ______ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊХзЮяЯпyЃНЉx2ЃЋbxЃЋcНЛyжсгкЕуAЃЈ0,4ЃЉЃЌНЛxжсгкЕуBЃЈ4,0ЃЉЃЌЕуPЪЧХзЮяЯпЩЯвЛЖЏЕуЃЌЙ§ЕуPзїxжсЕФДЙЯпPQЃЌЙ§ЕуAзїAQЁЭPQгкЕуQЃЌСЌНгAPЃЎ
ЃЈ1ЃЉЬюПеЃКХзЮяЯпЕФНтЮіЪНЮЊ ЃЌЕуCЕФзјБъ ЃЛ
ЃЈ2ЃЉЕуPдкХзЮяЯпЩЯдЫЖЏЃЌШєЁїAQPЁзЁїAOCЃЌЧѓЕуPЕФзјБъ.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЁбOЕФАыОЖЮЊ10ЃЌдВаФOЕНЯвABЕФОрРыЮЊ5ЃЌдђЯвABЫљЖдЕФдВжмНЧЕФЖШЪ§ЪЧЃЈЁЁЁЁЃЉ
A. 30Ёу B. 60Ёу C. 30ЁуЛђ150Ёу D. 60ЁуЛђ120Ёу
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
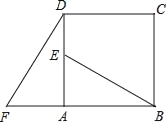
ЁОЬтФПЁПШчЭМЃЌЫФБпаЮABCDЪЧе§ЗНаЮЃЌЁїADFШЦзХЕуAЫГЪБа§зЊ90ЁуЕУЕНЁїABEЃЌШєAFЃН4ЃЌABЃН7ЃЎ
ЃЈ1ЃЉЧѓDEЕФГЄЖШЃЛ
ЃЈ2ЃЉжИГіBEгыDFЕФЙиЯЕШчКЮЃПВЂЫЕУїгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЪГЦЗСуЪлЕъЮЊЪГЦЗГЇДњЯњвЛжжУцАќЃЌЮДЪлГіЕФУцАќПЩвдЭЫЛиГЇМвЃЎОЭГМЦЯњЪлЧщПіЗЂЯжЃЌЕБетжжУцАќЕФЯњЪлЕЅМлЮЊ7НЧЪБЃЌУПЬьТєГі160ИіЃЎдкДЫЛљДЁЩЯЃЎЕЅМлУПЬсИп1НЧЪБЃЌИУСуЪлЕъУПЬьОЭЛсЩйТєГі20ИіУцАќЃЎЩшетжжУцАќЕФЯњЪлЕЅМлЮЊxНЧ(УПИіУцАќЕФГЩБОЪЧ5НЧ)ЃЎСуЪлЕъУПЬьЯњЪлетжжУцАќЕФРћШѓЮЊyНЧЃЎ
(1)гУКЌxЕФДњЪ§ЪНЗжБ№БэЪОГіУПИіУцАќЕФРћШѓгыТєГіЕФУцАќИіЪ§ЃЛ
(2)ЧѓxгыyжЎМфЕФКЏЪ§ЙиЯЕЪНЃК
(3)ЕБетжжУцАќЕФЯњЪлЕЅМлЖЈЮЊЖрЩйЪБЃЌИУСуЪлЕъУПЬьЯњЪлетжжУцАќЛёЕУЕФРћШѓзюДѓЃПзюДѓРћШѓЮЊЖрЩйдЊЃП
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com