
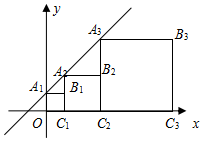
 如图,正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按照如图所示的方式放置,点A1,A2,A3,…和点C1,C2,C3,…分别在直线y=kx+b(k>0)和x轴上,已知点B1(1,1),B2(3,2),则B3的坐标是(7,4).
如图,正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按照如图所示的方式放置,点A1,A2,A3,…和点C1,C2,C3,…分别在直线y=kx+b(k>0)和x轴上,已知点B1(1,1),B2(3,2),则B3的坐标是(7,4). 分析 首先利用待定系数法求得直线A1A2的解析式,然后求得B3的坐标.
解答 解:∵B1的坐标为(1,1),点B2的坐标为(3,2),
∴正方形A1B1C1O1边长为1,正方形A2B2C2C1边长为2,
∴A1的坐标是(0,1),A2的坐标是:(1,2),
代入y=kx+b(k≠0)得:$\left\{\begin{array}{l}{b=1}\\{k+b=2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=1}\\{b=1}\end{array}\right.$,
则直线A1A2的解析式是:y=x+1.
∵A1B1=1,点B2的坐标为(3,2),
∴点A3的坐标为(3,4),
∴A3C2=A3B3=B3C3=4,
∴点B3的坐标为(7,4).
故答案为(7,4).
点评 此题考查了待定系数法求直线的解析式,一次函数图象上点的坐标特征以及正方形的性质,正确得到k与b的值是解题的关键.


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com