练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    12．在下列软件的图标中，其中是中心对称图形的有（　　）
    A．1个B．2个C．3个D．4个

    分析 根据轴对称图形的概念进行判断即可．

    解答 解：第一个图形不是中心对称图形；
    第二个图形不是中心对称图形；
    第三个图形是中心对称图形；
    第四个图形是中心对称图形，
    故选：B．

    点评 本题考查的是中心对称图形与轴对称图形的概念．轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合，中心对称图形是要寻找对称中心，旋转180度后两部分重合．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    2．在△ABC中，已知AC=5，且$\frac{1}{tan\frac{A}{2}}$+$\frac{1}{tan\frac{C}{2}}$-$\frac{5}{tan\frac{B}{2}}$=0，则BC+AB=（　　）
    A．6B．7C．8D．9

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

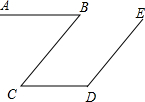    3．已知：如图所示，AB∥CD，∠B+∠D=180°．求证：BC∥DE
    证明：∵AB∥CD  已知
    ∴∠B=∠C（两直线平行，内错角相等）
    ∵∠B+∠D=180°已知
    ∴∠C+∠D=180°  （等量代换）
    ∴BC∥DE（同旁内角互补，两直线平行）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．完成证明，说明理由．已知：如图，BC∥DE，点E在AB边上，DE、AC交于点F，∠1=∠2，∠3=∠4，求证AE∥CD．
    证明：∵BC∥DE（已知），
    ∴∠4=∠FCB（两直线平行，同位角相等）．
    ∵∠3=∠4（已知），
    ∴∠3=∠FCB（等量代换）．
    ∵∠1=∠2（已知），
    ∴∠1+∠FCE=∠2+∠FCE（等式的性质）．
    即∠FCB=∠ECB，
    ∴∠3=∠ECD（等量代换）．
    ∴AE∥CD（内错角相等，两直线平行）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．在平面直角坐标系中，点A、B的坐标分别为（a，0），（0，b），其中a，b满足$\sqrt{a-2b-18}$+|2a-5b-30|=0．将点B向右平移26个单位长度得到点C，如图①所示．
    （1）求点A，B，C的坐标；
    （2）点M，N分别为线段BC，OA上的两个动点，点M从点C向左以1.5个单位长度/秒运动，同时点N从点O向点A以2个单位长度/秒运动，如图②所示，设运动时间为t秒（0＜t＜15）．
    ①当CM＜AN时，求t的取值范围；
    ②是否存在一段时间，使得S四边形MNOB＞2S四边形MNAC？若存在，求出t的取值范围；若不存在，说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    17．已知一个等腰三角形的两边长分别为$\sqrt{18}$和$\sqrt{50}$，则这个等腰三角形的周长为（　　）
    A．11$\sqrt{2}$B．13$\sqrt{2}$C．11$\sqrt{3}$或$\sqrt{3}$D．11$\sqrt{2}$或13$\sqrt{2}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    4．如图，每个图形都由同样大小的“”按照一定的规律组成，其中第1个图形有1个“”，第2个图形有2个“”，第3个图形有5个“”，…，则第6个图形中“”的个数为（　　）
    A．23B．24C．25D．26

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．如图1，将两个完全相同的三角形纸片ABC和DEC重合放置，其中∠C=90°，∠B=∠E=30°．
    （1）如图2，固定△ABC，将△DEC绕点C旋转，当点D恰好落在AB边上时，
    ①判断DE和AC的位置关系，并说明理由；
    ②设△BDC的面积为S1，△AEC的面积为S2，那么S1与S2的数量关系是S1=S2；

    （2）当△DEC绕点C旋转到图3所示的位置时，小明猜想（1）中S1与S2的数量关系仍然成立，并尝试分别作出了△BDC和△AEC中BC、CE边上的高，请你证明小明的猜想．
    （3）如图4，∠ABC=60°，点D在其角平分线上，BD=CD=6，DE∥AB交BC于点E，若点F在射线BA上，并且S△DCF=S△BDE，请直接写出相应的BF的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    2．已知方程$\frac{2kx+5}{k+x}=1$的根为x=1，则k=（　　）
    A．4B．-4C．1D．-1

    查看答案和解析>>

    同步练习册答案