
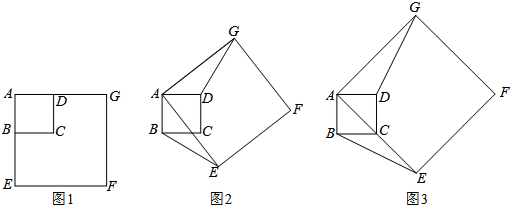
分析 (1)由旋转的性质得到∠BAE=∠DAG,由正方形的性质得到AB=AD,AE=AG,然后依据SAS可证明△ABE≌△ADG,然后依据全等三角形的性质进行证明即可;
(2)连接GE、BG,延长AD交GE与H.当α=45°时,可证明△AHE为等腰直角三角形,然后可求得AH和HE的长,然后依据等腰三角形三线合一的性质可得到EG=2HE,最后在△BEG中,利用面积法可求得点G到BE的距离.
解答 解:(1)由旋转的性质可知:∠BAE=∠DAG,由正方形的性质可知:AB=AD,AE=AG.
∵在△ABE和△ADG中,$\left\{\begin{array}{l}{AB=AD}\\{∠BAE=∠DAE}\\{AE=AG}\end{array}\right.$,
∴△ABE≌△ADG.
∴BE=DG.
(2)连接GE、BG,延长AD交GE与H.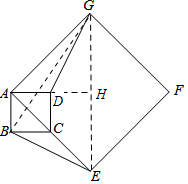
当α=45°时,则∠BAD=45°.
∵∠BAD=∠EAG=90°.
∴∠EAH=∠GAH=45°.
又∵AE=AG,
∴AH⊥GE.
又∵AH⊥AB,∠EAH=45°,
∴△AHE为等腰直角三角形.
∴EH=AH=$\frac{\sqrt{2}}{2}$AE=4.
∴EG=2EH=8.
∴S△BEG=$\frac{1}{2}$EG•AH=$\frac{1}{2}$×8×4=16.
设点G到BE的距离为h.
S△BEG=$\frac{1}{2}$EB•h=16,即$\frac{1}{2}$×4$\sqrt{2}$h=16,解得h=4$\sqrt{2}$.
∴点G到BE的距离为4$\sqrt{2}$.
点评 本题主要考查的是全等三角形的性质和判定、等腰直角三角形的性质和判定、矩形的性质,面积法的应用是解题的关键.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{x+y}{y}$=$\frac{5}{3}$ | B. | $\frac{y-x}{y}$=$\frac{1}{3}$ | C. | $\frac{x+1}{y+1}$=$\frac{3}{4}$ | D. | $\frac{x}{2y}$=$\frac{1}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
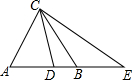 如图,△ABC中,AB=AC=8,D在AB上,E在AB的延长线上,∠ECB=∠DCB,AE=12.
如图,△ABC中,AB=AC=8,D在AB上,E在AB的延长线上,∠ECB=∠DCB,AE=12.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
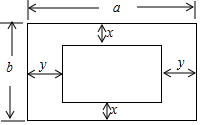 如图,内外两个四边形相似,且对应边互相平行,则下列结论正确的是( )
如图,内外两个四边形相似,且对应边互相平行,则下列结论正确的是( )| A. | $\frac{y}{x}$=1 | B. | $\frac{y}{x}$=$\frac{a}{b}$ | C. | $\frac{y}{x}$=$\frac{b}{a}$ | D. | 以上均不正确 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
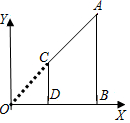 如图,AB,CD都垂直于x轴,垂足分别为B,D,若A(6,3),C(2,1),
如图,AB,CD都垂直于x轴,垂足分别为B,D,若A(6,3),C(2,1),| A. | 1:2 | B. | 1:3 | C. | 1:4 | D. | 1:8 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
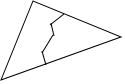 小丽不小心打碎了一块玻璃(如图),玻璃店老板根据涂总阴影部分重新划出一块与原来的玻璃完全相同的玻璃,其根据是( )
小丽不小心打碎了一块玻璃(如图),玻璃店老板根据涂总阴影部分重新划出一块与原来的玻璃完全相同的玻璃,其根据是( )| A. | SAS | B. | SSS | C. | ASA | D. | AAS |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com