
【题目】如图(1),![]() 的顶点
的顶点![]() 、
、![]() 、
、![]() 分别与正方形
分别与正方形![]() 的顶点
的顶点![]() 、
、![]() 、
、![]() 重合.
重合.
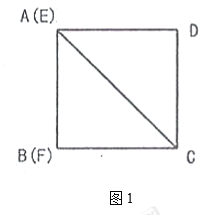
(1)若正方形的边长为![]() ,用含
,用含![]() 的代数式表示:正方形
的代数式表示:正方形![]() 的周长等于_______,
的周长等于_______,![]() 的面积等于_______.
的面积等于_______.
(2)如图2,将![]() 绕点
绕点![]() 顺时针旋转,边
顺时针旋转,边![]() 和正方形的边
和正方形的边![]() 交于点
交于点![]() .连结
.连结![]() ,设旋转角
,设旋转角![]() .
.

①试说明![]() ;
;
②若![]() 有一个内角等于
有一个内角等于![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() ,
,![]() ;(2)①见解析;②β=15°.
;(2)①见解析;②β=15°.
【解析】
(1)根据正方形的周长和等腰直角三角形的计算公式计算即可;
(2)①根据∠ECF和∠ACD都是45°即可说明;②首先判定△CAE是等腰三角形,明确∠β=∠ACE,再对![]() 的内角展开讨论,即可求得结果.
的内角展开讨论,即可求得结果.
解:(1)正方形![]() 的周长等于
的周长等于![]() ,
,![]() 的面积等于
的面积等于![]() .
.
故答案为![]() ,
,![]() ;
;
(2)①如图,∵![]() 的顶点
的顶点![]() 、
、![]() 、
、![]() 分别与正方形
分别与正方形![]() 的顶点
的顶点![]() 、
、![]() 、
、![]() 重合,
重合,
∴![]() 是等腰直角三角形,∴∠ECF=45°,
是等腰直角三角形,∴∠ECF=45°,
∵四边形ABCD是正方形,∴∠ACD=45°,
即∠ACF+∠1=45°,∠DCP+∠1=45°,
∴![]() .
.

②∵CA=CE,∴∠CAE=∠CEA,且∠CAE<90°,
若∠PAE=60°,则∠CAE=45°+60°=105°>90°,不符合题意;
若∠APE=60°,则∠APC=120°,∴∠1=180°―120°―45°=15°,∴∠BCF=∠1=15°,即旋转角β=15°;
若∠AEP=60°,则∠CAE=60°,所以∠1=60°>45°,此时点P在AD的延长线上,与题意中“边![]() 和正方形的边
和正方形的边![]() 交于点
交于点![]() ”相矛盾,不符合题意;
”相矛盾,不符合题意;
综上,旋转角β=15°.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
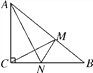
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm.动点M从点B出发,在BA边上以每秒3cm的速度向定点A运动,同时动点N从点C出发,在CB边上以每秒2cm的速度向点B运动,运动时间为t秒![]() ,连接MN.
,连接MN.
(1)若△BMN与△ABC相似,求t的值;
(2)连接AN,CM,若AN⊥CM,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列图形都是由同样大小的黑色圆点按照一定规律所组成的,其中第①个图形中一共有6个黑色圆点第②个图形中一共有15个黑色圆点,第③个图形中一共有28个黑色圆点,…,按此规律排列下去,第⑦个图形中黑色圆点的个数为( )

A.66B.91C.120D.135
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和几位同学做手的影子游戏时,发现对于同一物体,影子的大小与光源到物体的距离有关.因此,他们认为:可以借助物体的影子长度计算光源到物体的位置.于是,他们做了以下尝试.
(1)如图①,垂直于地面放置的正方形框架ABCD,边长AB为30cm,在其正上方有一灯泡,在灯泡的照射下,正方形框架的横向影子A′B,D′C的长度和为6cm.那么灯泡离地面的高度为 .
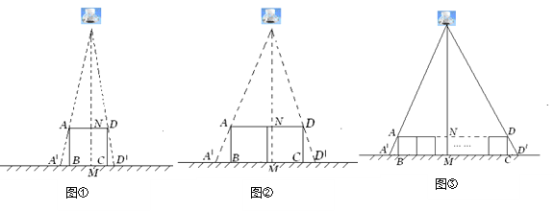 (2)不改变①中灯泡的高度,将两个边长为30cm的正方形框架按图②摆放,请计算此时横向影子A′B,D′C的长度和为多少?
(2)不改变①中灯泡的高度,将两个边长为30cm的正方形框架按图②摆放,请计算此时横向影子A′B,D′C的长度和为多少?
(3)有n个边长为a的正方形按图③摆放,测得横向影子A′B,D′C的长度和为b,求灯泡离地面的距离.(写出解题过程,结果用含a,b,n的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某种车的耗油量,我们对这种车做了试验,并把试验的数据记录下来,制成下表:
汽车行驶时间t(h) | 0 | 1 | 2 | 3 | ······ |
剩余油量Q(L) | 50 | 44 | 38 | 32 | ······ |
(1)根据上表的数据,能用t表示Q吗?试一试;
(2)汽车行驶5h后,油箱中的剩余油量是多少?
(3)若汽车油箱中剩余油量为14L,则汽车行使了多少小时?
(4)贮满50L汽油的汽车,最多行驶几小时?
查看答案和解析>>
科目:初中数学 来源: 题型:
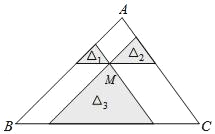
【题目】如图,点M是△ABC内一点,过点M分别作直线平行于△ABC的各边,所形成的三个小三角形△1、△2、△3(图中阴影部分)的面积分别是1、4、25.则△ABC的面积是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CA⊥AB,DB⊥AB,已知AC=2,AB=6,点P射线BD上一动点,以CP为直径作⊙O,点P运动时,若⊙O与线段AB有公共点,则BP最大值为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,二次函数y1=(x﹣2)(x﹣4)的图象与x轴交于A、B两点(点A在点B的左侧),其对称轴l与x轴交于点C,它的顶点为点D.
(1)写出点D的坐标 .
(2)点P在对称轴l上,位于点C上方,且CP=2CD,以P为顶点的二次函数y2=ax2+bx+c(a≠0)的图象过点A.
①试说明二次函数y2=ax2+bx+c(a≠0)的图象过点B;
②点R在二次函数y1=(x﹣2)(x﹣4)的图象上,到x轴的距离为d,当点R的坐标为 时,二次函数y2=ax2+bx+c(a≠0)的图象上有且只有三个点到x轴的距离等于2d;
③如图2,已知0<m<2,过点M(0,m)作x轴的平行线,分别交二次函数y1=(x﹣2)(x﹣4)y2=ax2+bx+c(a≠0)的图象于点E、F、G、H(点E、G在对称轴l左侧),过点H作x轴的垂线,垂足为点N,交二次函数y1=(x﹣2)(x﹣4)的图象于点Q,若△GHN∽△EHQ,求实数m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着科技的发展,某快递公司为了提高分拣包裹的速度,使用机器人代替人工进行包裹分拣,若甲机器人工作![]() ,乙机器人工作
,乙机器人工作![]() ,一共可以分拣700件包裹;若甲机器人工作
,一共可以分拣700件包裹;若甲机器人工作![]() ,乙机器人工作
,乙机器人工作![]() ,一共可以分拣650件包裹.
,一共可以分拣650件包裹.
(1)求甲、乙两机器人每小时各分拣多少件包裹;
(2)去年“双十一”期间,快递公司的业务量猛增,为了让甲、乙两机器人每天分拣包裹的总数量不低于2250件,则它们每天至少要一起工作多少小时?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com