
【题目】(1)某学校“智慧方园”数学社团遇到这样一个题目:
如图1,在![]() 中,点
中,点![]() 在线段
在线段![]() 上,
上,![]() ,
,![]() ,
,![]() ,
,![]() ,求
,求![]() 的长.
的长.
经过社团成员讨论发现,过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,通过构造
,通过构造![]() 就可以解决问题(如图
就可以解决问题(如图![]() .
.
请回答:![]()
![]() ,
,![]() .
.
(2)请参考以上解决思路,解决问题:
如图3,在四边形![]() 中,对角线
中,对角线![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,求
,求![]() 的长.
的长.

【答案】(1) 75°;4![]() (2)
(2)![]()
【解析】
(1)根据平行线的性质可得出∠ADB=∠OAC=75°,结合∠BOD=∠COA可得出△BOD∽△COA,利用相似三角形的性质可求出OD的值,进而可得出AD的值,由三角形内角和定理可得出∠ABD=75°=∠ADB,由等角对等边可得出AB=AD=4![]() ,此题得解;
,此题得解;
(2)过点B作BE∥AD交AC于点E,同(1)可得出AE=4![]() ,在Rt△AEB中,利用勾股定理可求出BE的长度,再在Rt△CAD中,利用勾股定理可求出DC的长,此题得解.
,在Rt△AEB中,利用勾股定理可求出BE的长度,再在Rt△CAD中,利用勾股定理可求出DC的长,此题得解.
解:(1)∵BD∥AC,
∴∠ADB=∠OAC=75°.
∵∠BOD=∠COA,
∴△BOD∽△COA,
∴![]() .
.
又∵AO=3![]() ,
,
∴OD=![]() AO=
AO=![]() ,
,
∴AD=AO+OD=4![]() .
.
∵∠BAD=30°,∠ADB=75°,
∴∠ABD=180°-∠BAD-∠ADB=75°=∠ADB,
∴AB=AD=4![]()
故答案为:75;4![]() .
.
(2)过点B作BE∥AD交AC于点E,如图所示.
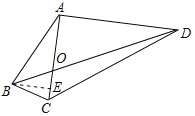
∵AC⊥AD,BE∥AD,
∴∠DAC=∠BEA=90°.
∵∠AOD=∠EOB,
∴△AOD∽△EOB,
∴![]() .
.
∵BO:OD=1:3,
∴![]()
∵AO=3![]() ,
,
∴EO=![]() ,
,
∴AE=4![]()
∵∠ABC=∠ACB=75°,
∴∠BAC=30°,AB=AC,
∴AB=2BE.
在Rt△AEB中,BE2+AE2=AB2,即(4![]() )2+BE2=(2BE)2,
)2+BE2=(2BE)2,
解得:BE=4,
∴AB=AC=8,AD=12.
在Rt△CAD中,AC2+AD2=CD2,即82+122=CD2,
解得:CD=4![]() .
.


科目:初中数学 来源: 题型:
【题目】已知:二次函数y=ax2+2ax﹣4(a≠0)的图象与x轴交于点A,B(A点在B点的左侧),与y轴交于点C,△ABC的面积为12.
(1)求二次函数图象的对称轴与它的解析式;
(2)点D在y轴上,当以A、O、D为顶点的三角形与△BOC相似时,求点D的坐标;
(3)点D的坐标为(﹣2,1),点P在二次函数图象上,∠ADP为锐角,且tan∠ADP=2,求点P的横坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴的原点为O,点A、B、C是数轴上的三点,点B对应的数为1,AB=8,BC=3,动点P、Q同时从A、C出发,分别以每秒2个长度单位和每秒1个长度单位的速度沿数轴正方向运动.设运动时间为t秒(t>0)
(1)求点A、C分别对应的数;
(2)求点P、Q分别对应的数;(用含t的式子表示)
(3)试问当t为何值时,OP=OQ?
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校有3000名学生.为了解全校学生的上学方式,该校数学兴趣小组以问卷调查的形式,随机调查了该校部分学生的主要上学方式(参与问卷调查的学生只能从以下六个种类中选择一类),并将调查结果绘制成如下不完整的统计图.
种类 | A | B | C | D | E | F |
上学方式 | 电动车 | 私家车 | 公共交通 | 自行车 | 步行 | 其他 |
某校部分学生主要上学方式扇形统计图某校部分学生主要上学方式条形统计图

根据以上信息,回答下列问题:
(1)参与本次问卷调查的学生共有____人,其中选择B类的人数有____人.
(2)在扇形统计图中,求E类对应的扇形圆心角α的度数,并补全条形统计图.
(3)若将A、C、D、E这四类上学方式视为“绿色出行”,请估计该校每天“绿色出行”的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC为锐角三角形,AD是BC边上的高,正方形EFMN的一边MN在边BC上,顶点E、F分别在AB、AC上,其中BC=24cm,高AD=12cm.
(1)求证:△AEF∽△ABC:
(2)求正方形EFMN的边长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:点O到△ABC的两边AB、AC所在直线的距离相等,且OB=OC.
(1)如图1,若点O在BC上,求证:AB=AC;
(2)如图2,若点O在△ABC的内部,求证:AB=AC.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标平面内,已知点![]() 的坐标
的坐标![]() ,点
,点![]() 位置如图所示,点
位置如图所示,点![]() 与点
与点![]() 关于原点对称。
关于原点对称。
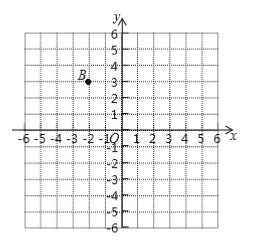
(1)在图中描出点![]() ;写出图中点
;写出图中点![]() 的坐标:______________,点
的坐标:______________,点![]() 的坐标:_______________;
的坐标:_______________;
(2)画出![]() 关于
关于![]() 轴的对称图形
轴的对称图形![]() ,并求出四边形
,并求出四边形![]() 的面积。
的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,点A(1,0),B(4,1),C(4,3),反比例函数y=![]() 的图象经过点D,点P是一次函数y=mx+3﹣4m(m≠0)的图象与该反比例函数图象的一个公共点;
的图象经过点D,点P是一次函数y=mx+3﹣4m(m≠0)的图象与该反比例函数图象的一个公共点;
(1)求反比例函数的解析式;
(2)通过计算说明一次函数y=mx+3﹣4m的图象一定过点C;
(3)对于一次函数y=mx+3﹣4m(m≠0),当y随x的增大而增大时,确定点P的横坐标的取值范围,(不必写过程)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用正方形硬纸板做三棱柱盒子,每个盒子由3个矩形侧面和2个正三角形底面组成。硬纸板以如图两种方式裁剪(裁剪后边角料不再利用)
A方法:剪6个侧面; B方法:剪4个侧面和5个底面。

现有19张硬纸板,裁剪时![]() 张用A方法,其余用B方法。
张用A方法,其余用B方法。
(1)用![]() 的代数式分别表示裁剪出的侧面和底面的个数;
的代数式分别表示裁剪出的侧面和底面的个数;
(2)若裁剪出的侧面和底面恰好全部用完,问能做多少个盒子?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com