
【题目】如图,在Rt△ABC中,∠C=90°,∠A=60°,AB=12cm,若点P从点B出发以2cm/s的速度向点A运动,点Q从点A出发以1cm/s的速度向点C运动,设P、Q分别从点B、A同时出发,运动的时间为ts. 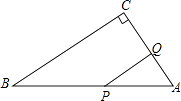
(1)用含t的式子表示线段AP、AQ的长;
(2)当t为何值时,△APQ是以PQ为底边的等腰三角形?
(3)当t为何值时,PQ∥BC?
【答案】
(1)解:∵Rt△ABC中,∠C=90°,∠A=60°,
∴∠B=30°.
又∵AB=12cm,
∴AC=6cm,BP=2t,AP=AB﹣BP=12﹣2t,AQ=t
(2)解:∵△APQ是以PQ为底的等腰三角形,
∴AP=AQ,即12﹣2t=t,
∴当t=4时,△APQ是以PQ为底边的等腰三角形
(3)解:当PQ⊥AC时,PQ∥BC.
∵∠C=90°,∠A=60°,
∴∠B=30°
∵PQ∥BC,
∴∠QPA=30°
∴AQ= ![]() AP,
AP,
∴t= ![]() (12﹣2t),解得t=3,
(12﹣2t),解得t=3,
∴当t=3时,PQ∥BC
【解析】(1)由题意,可知∠B=30°,AC=6cm.BP=2t,AP=AB﹣BP,AQ=t.(2)若△APQ是以PQ为底的等腰三角形,则有AP=AQ,即12﹣2t=t,求出t即可.(3)先根据直角三角形的性质求出∠B的度数,再由平行线的性质得出∠QPA的度数,根据直角三角形的性质即可得出结论.
【考点精析】认真审题,首先需要了解平行线的判定(同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行),还要掌握等腰三角形的判定(如果一个三角形有两个角相等,那么这两个角所对的边也相等(简称:等角对等边).这个判定定理常用于证明同一个三角形中的边相等)的相关知识才是答题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】小明的作业本上有四道利用不等式的性质,将不等式化为x>a或x<a的作业题:①由x+7>8解得x>1;②由x<2x+3解得x<3;③由3x-1>x+7解得x>4;④由-3x>-6解得x<-2.其中正确的有( )
A. 1题 B. 2题
C. 3题 D. 4题
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种细胞开始有2个,1小时后分裂成4个并死去1个,2小时分裂成6个并死去1个,3小时后分裂成10个并死去1个,按此规律,5小时后细胞存活的个数是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】求21+22+23+…+2n的和,解法如下: 解:设S=21+22+23+…+2n①
2S=22+23+…+2n+2n+1②
②﹣①得S=2n+1﹣2
所以21+22+23+…+2n=2n+1﹣2
参照上面的解法,
计算:1+31+32+33+…+3n﹣1= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,将ABCD放置在第一象限,且AB∥x轴.直线y=﹣x从原点出发沿x轴正方向平移,在平移过程中直线被平行四边形截得的线段长度l与直线在x轴上平移的距离m的函数图象如图2所示,那么AD的长为 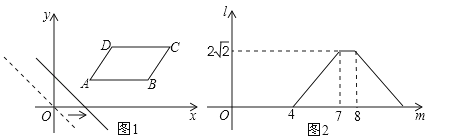
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com