
如下图,一块铁皮呈锐角三角形,它的边
BC=80 cm,高AD=60 cm.要把它加工成矩形零件,并且矩形长的一边位于边BC上,另两个顶点分别在边AB、AC上,试确定矩形零件的最大面积.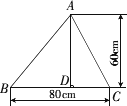
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:初中数学 三点一测丛书 八年级数学 下 (江苏版课标本) 江苏版 题型:044
“三等分角”是数学史上一个著名问题,但仅用尺规不可能“三等分角”.下面是数学家帕普斯借助函数给出的一种“三等分锐角”的方法(如下图).将给定的锐角∠AOB置于直角坐标系中,边OB在x轴上、边OA与函数y=![]() 的图像交于点P,以P为圆心、以2OP为半径作弧交图像于点R.分别过点P和R作x轴和y轴的平行线,两直线相交于点M,连结OM得到∠MOB,则∠MOB=
的图像交于点P,以P为圆心、以2OP为半径作弧交图像于点R.分别过点P和R作x轴和y轴的平行线,两直线相交于点M,连结OM得到∠MOB,则∠MOB=![]() ∠AOB.
∠AOB.

要明白帕普斯的方法,请研究以下问题:
(1)设P![]() 、R
、R![]() ,求直线OM对应的函数表达式(用含a,b的代数式表示);
,求直线OM对应的函数表达式(用含a,b的代数式表示);
(2)分别过点P和R作y轴和x轴的平行线,两直线相交于点Q.请说明Q点在直线OM上,并据此证明∠MOB=![]() ∠AOB;
∠AOB;
(3)应用上述方法得到的结论,你如何三等分一个钝角(用文字简要说明).
查看答案和解析>>
科目:初中数学 来源:学习周报 数学 沪科九年级版 2009-2010学年 第7期 总第163期 沪科版 题型:044
课本典型题展示:如下图,一块铁皮呈锐角三角形,它的边
BC=80 cm,高AD=60 cm.要把它加工成矩形零件,使矩形的长、宽之比为2∶1,并且矩形长的一边位于边BC上,另两个顶点分别在边AB、AC上,求这个矩形零件的长与宽.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,一块边缘呈抛物线型的铁片如图放置,测得![]() ,抛物线的顶点到
,抛物线的顶点到![]() 边的距离为
边的距离为![]() .现要沿
.现要沿![]() 边向上依次截取宽度均为
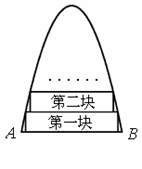
边向上依次截取宽度均为![]() 的矩形铁皮,如图所示.已知截得的铁皮中有一块是正方形,则这块正方形铁皮是( )。
的矩形铁皮,如图所示.已知截得的铁皮中有一块是正方形,则这块正方形铁皮是( )。
A.第七块 B.第六块 C.第五块 D.第四块
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com