
分析 (1)首先提公因式4,然后把前三项写成完全平方的形式,利用平方差公式分解;
(2)首先利用平方差公式以及单项式与多项式的乘法、单项式与单项式的除法法则计算,然后合并同类项即可;
(3)首先把括号内的分式的分母分解因式,把除法转化为乘法,然后利用分配律计算,最后进行分式的加减即可;
(4)首先去分母转化为整式方程求得x的值,然后进行检验即可.
解答 解:(1)原式=4(a2-2ab+b2-4c2)
=4[(a2-2ab+b2)-4c2]=4[(a-b)2-4c2]
=4(a-b+2c)(a-b-2c);
(2)原式=4a4-b2+2ab+b2-4a2=2ab;
(3)原式=[$\frac{3x+4}{(x+1)(x-1)}$-$\frac{2}{x-1}$]÷$\frac{x+2}{(x-1)^{2}}$
=$\frac{3x+4}{(x+1)(x-1)}$•$\frac{(x-1)^{2}}{x+2}$-$\frac{2}{x-1}$•$\frac{(x-1)^{2}}{x+2}$
=$\frac{(3x+4)(x-1)}{(x-1)(x+2)}$-$\frac{2(x-1)^{2}}{(x-1)(x+2)}$
=$\frac{(3x+4)(x-1)-2(x-1)^{2}}{(x-1)(x+2)}$
=$\frac{(x-1)[(3x+4)-2(x-1)]}{(x-1)(x+2)}$
=$\frac{3x+4-2(x-1)}{x+2}$
=$\frac{x+2}{x+2}$
=1;
(4)方程两边同时乘以(x+2)(x-2)得,x(x+2)-(x2-4)=8,
去括号,得x2+2x-x2-4=8,
解得:x=6,
检验:当x=6时,(x+2)(x-2)=8×4=32≠0.
则x=6是方程的解.
点评 本题考查了分式的化简求值以及分式方程的解法,正确进行分解因式是关键,且要注意解分式方程时一定要检验.


 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案科目:初中数学 来源: 题型:填空题
 将正整数按如图所示的规律排列下去,若用有序实数对(n,m)表示第n排,从左到右第m个数,如(4,3)表示实数9,则(11,5)表示的实数是60.
将正整数按如图所示的规律排列下去,若用有序实数对(n,m)表示第n排,从左到右第m个数,如(4,3)表示实数9,则(11,5)表示的实数是60.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
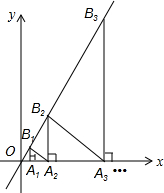 如图,在坐标轴上取点A1(2,0),作x轴的垂线与直线y=2x交于点B1,作等腰直角三角形A1B1A2;又过点A2作x轴的垂线交直线y=2x交于点B2,作等腰直角三角形A2B2A3;…,如此反复作等腰直角三角形,当作到An(n为正整数)点时,则An的坐标是(2×3n-1,0).
如图,在坐标轴上取点A1(2,0),作x轴的垂线与直线y=2x交于点B1,作等腰直角三角形A1B1A2;又过点A2作x轴的垂线交直线y=2x交于点B2,作等腰直角三角形A2B2A3;…,如此反复作等腰直角三角形,当作到An(n为正整数)点时,则An的坐标是(2×3n-1,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{3}{2}$ | C. | $\frac{2}{5}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com