【题目】如图，将△ABC沿它的中位线MN折叠后，点A落在点A′处，若∠A=30°，∠B=115°，则∠A′NC=°．
【答案】110
【解析】解：∵∠A=30°，∠B=115°，
∴∠C=180°﹣∠A﹣∠B=180°﹣30°﹣115°=35°，
∵MN是三角形的中位线，
∴MN∥BC，
∴∠A′NM=∠C=35°，∠CNM=180°﹣∠C=180°﹣35°=145°，
∴∠A′NC=∠CNM﹣∠A′NM=145°﹣35°=110°．
所以答案是：110．
【考点精析】解答此题的关键在于理解三角形中位线定理的相关知识，掌握连接三角形两边中点的线段叫做三角形的中位线；三角形中位线定理：三角形的中位线平行于三角形的第三边，且等于第三边的一半，以及对翻折变换（折叠问题）的理解，了解折叠是一种对称变换，它属于轴对称，对称轴是对应点的连线的垂直平分线，折叠前后图形的形状和大小不变，位置变化，对应边和角相等．
科目：初中数学 来源： 题型：
【题目】据媒体报道，我国最新研制的“察打一体”无人机的速度极快，经测试最高速度可达204000米/分，这个数用科学记数法表示，正确的是（ ）
A.204×103
B.20.4×104
C.2.04×105
D.2.04×106
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，四边形ABCD中，对角线AC与BD相交于点O，不能判断四边形ABCD是平行四边形的是（ ） 
A.AB∥DC，AO=CO
B.AB∥DC，∠ABC=∠ADC
C.AB=DC，AD=BC
D.AB=DC，∠ABC=∠ADC
查看答案和解析>>
科目：初中数学 来源： 题型：
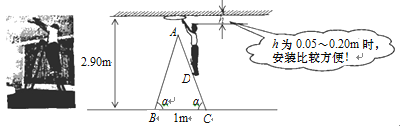
【题目】如图所示，电工李师傅借助梯子安装天花板上距地面2.90m的顶灯。已知梯子由两个相同的矩形面组成，每个矩形面的长都被六条踏板七等分，使用时梯脚的固定跨度为1m。矩形面与地面所成的角
为
。李师傅的身高为1.78m，当他攀升到头顶距天花板0.05～0.20m时，安装起来比较方面。
（1）求每条踏板间的垂直高度。
（2）请问他站立在梯子的第几级踏板上安装比较方便？请你通过计算判断说明。（参与数据：sin
，cos
，tan
）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系中，已知△ABC三个顶点的坐标分别为A(1，2)，B(3，4)，C(2，9)。
（1）画出△ABC关于y轴对称的△A1B1C1。
（2）画出△A1B1C1向右平移8个单位后得到的△A2B2C2。
（3）直接写出△ABC上点M(x，y)在上述变换过程中得到△A2B2C2上的对应点M2的坐标。
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（10分）在△ABC中，BE、CF分别是AC、AB两条边上的高，在BE上截取BD＝AC，在CF的延长线上截取CG＝AB，连结AD、AG。求证：AG＝AD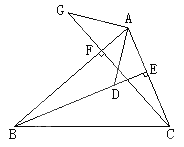
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在Rt△ABC中，∠ACB=90°，∠B=30°，AD平分∠CAB．
（1）求∠CAD的度数；
（2）延长AC至E，使CE=AC，求证：DA=DE．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】水产养殖专业户王大爷承包了30亩水塘，分别养殖甲鱼和桂鱼．有关成本、销售额见右表：
（1）2012年，王大爷养殖甲鱼20亩，桂鱼10亩．求王大爷这一年共收益多少万元？（收益＝销售额－成本）
（2）2013年，王大爷继续用这30亩水塘全部养殖甲鱼和桂鱼，计划投入成本不超过70万元．若每亩养殖的成本、销售额与2012年相同，要获得最大收益，他应养殖甲鱼和桂鱼各多少亩？
（3）已知甲鱼每亩需要饲料500kg，桂鱼每亩需要饲料700kg．根据(2)中的养殖亩数，为了节约运输成本，实际使用的运输车辆每次装载饲料的总量是原计划每次装载总量的2倍，结果运输养殖所需全部饲料比原计划减少了2次．求王大爷原定的运输车辆每次可装载饲料多少kg?
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中有一菱形OABC且∠A=120°，点O、B在y轴上，OA=1，现在把菱形向右无滑动翻转，每次翻转60°，点B的落点依次为B1、B2、B3…，连续翻转2017次，则B2017的坐标为_____．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com