
 如图,正方形ABCD、DEFH的边长都是5cm,点P从点D出发,先到点A,然后沿箭头所指方向运动(经过点D时不拐弯),则从出发开始连续运动2014cm时,它离点C 最近,此时它距该点1cm.
如图,正方形ABCD、DEFH的边长都是5cm,点P从点D出发,先到点A,然后沿箭头所指方向运动(经过点D时不拐弯),则从出发开始连续运动2014cm时,它离点C 最近,此时它距该点1cm. 分析 由题意可知:P点从D点出发,经过8条边又回到D点,即P点运动的周期为8条边,据此求出P点连续运动2014厘米,转过的正方形的边数,从而求出P点到达的位置,做出判断.
解答 解:P点从D点出发,经过8条边又回到D点,即P点运动的周期为8条边,
连续运动2014厘米,共运动的正方形的边数为:2014÷5=402(条)…4(厘米),
也就是运动了402条边后,又往前运动了4厘米;
402÷8=50(个周期)…2(条边),P点这时运动到D点后,又向前运动了2条边,到达B点;
∵P点运动了402条边后,又往前运动了4厘米,
∴应超过B点4厘米,应在距离C点5-4=1厘米处.
综上,P点离C点最近,此时它距该点1cm.
故答案为:C,1.
点评 本题考查图形的变化规律,观察出运动一个周期为8条边是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
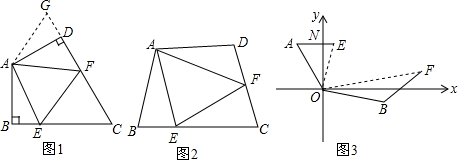
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
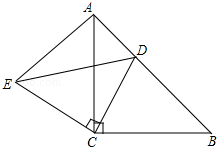 已知,如图,△ABC和△ECD都是等腰直角三角形,∠ACD=∠DCE=90°,D为AB边上一点.猜想BD2、AD2、CD2之间的关系,并证明.
已知,如图,△ABC和△ECD都是等腰直角三角形,∠ACD=∠DCE=90°,D为AB边上一点.猜想BD2、AD2、CD2之间的关系,并证明.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在?ABCD中,已知AB=a,BC=b,∠ABC=α
如图,在?ABCD中,已知AB=a,BC=b,∠ABC=α查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com