
【题目】已知:如图,AB为半圆O的直径,C、D是半圆O上的两点,若直径AB的长为4,且BC=2,∠DAC=15°.
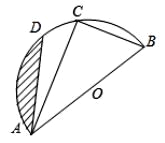
(1)求∠DAB的度数;
(2)求图中阴影部分的面积(结果保留π)
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:初中数学 来源: 题型:
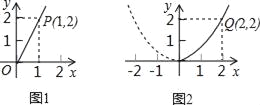
【题目】某园林专业户计划投资种植花卉及树木,根据市场调查与预测,种植树木的利润y与投资量x成正比例关系,如图1所示:种植花卉的利润y与投资量x成二次函数关系,如图2所示(注:利润与投资量的单位:万元)
(1)分别求出利润y1与y2关于投资量x的函数关系式;
(2)如果这位专业户以8万元资金投入种植花卉和树木,他至少获得多少利润?他能获取的最大利润是多少?
(3)在(2)的基础上要保证获利在22万元以上,该园林专业户应怎样投资?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,污水处理公司为某楼房建一座周长为30米的三级污水处理池,平面图为矩形![]() ,
,![]() 米,中间两条隔墙分别为
米,中间两条隔墙分别为![]() 、
、![]() ,池墙的厚度不考虑.
,池墙的厚度不考虑.
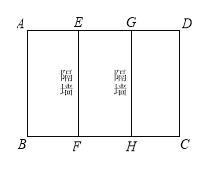
(1)用含![]() 的代数式表示外围墙
的代数式表示外围墙![]() 的长度;
的长度;
(2)如果设计时要求矩形水池![]() 恰好被隔墙分成三个全等的矩形,且它们均与矩形
恰好被隔墙分成三个全等的矩形,且它们均与矩形![]() 相似,求此时
相似,求此时![]() 的长;
的长;
(3)如果设计时要求矩形水池![]() 恰好被隔墙分成三个全等的正方形.已知池的外围墙建造单价为每米400元,中间两条隔墙建造单价每米300元,池底建造的单价为每平方米100元.试计算此项工程的总造价.(结果精确到1元)
恰好被隔墙分成三个全等的正方形.已知池的外围墙建造单价为每米400元,中间两条隔墙建造单价每米300元,池底建造的单价为每平方米100元.试计算此项工程的总造价.(结果精确到1元)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,直径BD交AC于E,过O作FG⊥AB,交AC于F,交AB于H,交⊙O于G.
(1)求证:OFDE=OE2OH;
(2)若⊙O的半径为12,且OE:OF:OD=2:3:6,求阴影部分的面积.(结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,将正方形OABC绕点O逆时针旋转45°后得到正方形OA1B1C1 , 依此方式,绕点O连续旋转2018次得到正方形OA2018B2018C2018 , 如果点A的坐标为(![]() ,0),那么点B2018的坐标为( )
,0),那么点B2018的坐标为( )

A. (1,1) B. (0,![]() ) C. (﹣1,1) D. (-
) C. (﹣1,1) D. (-![]() ,0)
,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于二次函数y=x2-3x+2和一次函数y=-2x+4,把y=t(x2-3x+2)+(1-t)(-2x+4)称为这两个函数的“再生二次函数”,其中t是不为零的实数,其图象记作抛物线L.现有点A(2,0)和抛物线L上的点B(-1,n),请完成下列任务:
(1)(尝试)
当t=2时,抛物线y=t(x2-3x+2)+(1-t)(-2x+4)的顶点坐标为________;
(2)判断点A是否在抛物线L上;
(3)求n的值.
(4)(发现)
通过(2)和(3)的演算可知,对于t取任何不为零的实数,抛物线L总过定点,坐标为________.
(5)(应用)
二次函数y=-3x2+5x+2是二次函数y=x23x+2和一次函数y=-2x+4的一个“再生二次函数”吗?如果是,求出t的值;如果不是,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
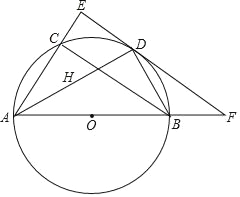
【题目】如图,在直角三角形ABC中,∠ACB=90°,点H是△ABC的内心,AH的延长线和三角形ABC的外接圆O相交于点D,连结DB.
(1)求证:DH=DB;
(2)过点D作BC的平行线交AC、AB的延长线分别于点E、F,已知CE=1,圆O的直径为5.
①求证:EF为圆O的切线;
②求DF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com