
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=60°,AC=2![]() ,点P为AB边上的一个动点,连接PC,过点P作PQ⊥PC交BC边于点Q,则BQ的最大值为_____.
,点P为AB边上的一个动点,连接PC,过点P作PQ⊥PC交BC边于点Q,则BQ的最大值为_____.
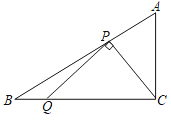
【答案】2
【解析】
过Q作QE⊥AB于E,过C作CF⊥AB于F,利用相似三角形的性质根据一元二次方程,利用根的判别式解决问题即可.
解:过Q作QE⊥AB于E,过C作CF⊥AB于F,
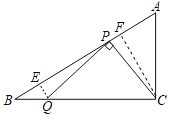
∵在Rt△ABC中,∠ACB=90°,∠A=60°,AC=2![]() ,
,
∴∠B=30°,
∴AB=2AC=4![]() ,BC=
,BC=![]() AC=6,
AC=6,
∵∠AFC=90°,∠A=60°,
∴∠ACF=30°,
∴AF=![]() ,CF=3,
,CF=3,
设PF=x,BQ=y,
∴QE=![]() BQ=
BQ=![]() y,BE=
y,BE=![]() y,
y,
∴PE=3![]() ﹣
﹣![]() y﹣x,
y﹣x,
∵PQ⊥PC,
∴∠PEQ=∠CFP=∠CPQ=90°,
∴∠EQP+∠EPQ=∠EPQ+∠CPF=90°,
∴∠PQE=∠CPF,
∴△PEQ∽△CFP,
∴![]() ,
,
∴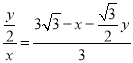
∴x2+(![]() y﹣3
y﹣3![]() )x+
)x+![]() =0,
=0,
∵方程有实数解,
∴△≥0,
∴(![]() y﹣3
y﹣3![]() )2﹣6y≥0,
)2﹣6y≥0,
整理得,y2﹣20y+36≥0,
解得y≤2或y≥18(舍弃),
∴BQ≤2,
∴BQ的最大值为2.
故答案为2.


 小学课时特训系列答案
小学课时特训系列答案科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的顶点
的顶点![]() 的坐标为
的坐标为![]() .
.
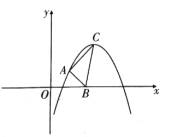
(1)求![]() ,
,![]() 的值;
的值;
(2)已知![]() 点为抛物线上异于
点为抛物线上异于![]() 的一点,且
的一点,且![]() 点横、纵坐标相等,
点横、纵坐标相等,![]() 为
为![]() 轴上任意一点,当
轴上任意一点,当![]() 取最小值时,求出
取最小值时,求出![]() 点坐标和此时
点坐标和此时![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形![]() 是正方形,点
是正方形,点![]() 的坐标是
的坐标是![]() .
.
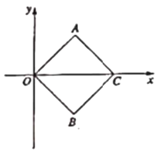
(1)正方形![]() 的边长为 ,点
的边长为 ,点![]() 的坐标是 ;
的坐标是 ;
(2)将正方形![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() ,点
,点![]() ,
,![]() ,
,![]() 旋转后的对应点为
旋转后的对应点为![]() ,
,![]() ,
,![]() ,求点
,求点![]() 的坐标及旋转后的正方形与原正方形的重叠部分的面积;
的坐标及旋转后的正方形与原正方形的重叠部分的面积;
(3)动点![]() 从点
从点![]() 出发,沿折线
出发,沿折线![]() 方向以1个单位/秒的速度匀速运动,同时,另一动点
方向以1个单位/秒的速度匀速运动,同时,另一动点![]() 从点
从点![]() 出发,沿折线
出发,沿折线![]() 方向以2个单位/秒的速度匀速运动,运动时间为
方向以2个单位/秒的速度匀速运动,运动时间为![]() 秒,当它们相遇时同时停止运动,当
秒,当它们相遇时同时停止运动,当![]() 为等腰三角形时,求出
为等腰三角形时,求出![]() 的值(直接写出结果即可).
的值(直接写出结果即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年11月22日,教育部发布关于《中小学教师实施教育惩戒规则(征求意见稿)》公开征求意见的通知,征求意见稿指出;教育惩戒是教师履行救育教学职责的必要手段和法定职权.教育惩戒分为![]() :一般惩戒,
:一般惩戒,![]() :较重惩戒,
:较重惩戒,![]() :严重惩戒,
:严重惩戒,![]() :强制措施,共四个层次.为了解家长对教育惩戒的看法,某中学对学生家长进行了随机调查,要求每位家长选择其中最关注的一个层次提出意见,学校对收集的信息进行统计,绘制了下面两幅不完整的统计图.
:强制措施,共四个层次.为了解家长对教育惩戒的看法,某中学对学生家长进行了随机调查,要求每位家长选择其中最关注的一个层次提出意见,学校对收集的信息进行统计,绘制了下面两幅不完整的统计图.

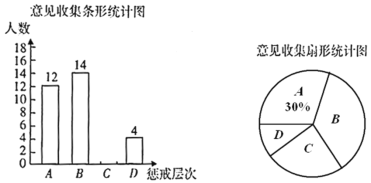
请你根据统计图提供的信息,解答下列问题:
(1)被调查的总人数是______人;
(2)扇形统计图中![]() 部分对应的圆心角的度数为______;
部分对应的圆心角的度数为______;
(3)补全条形统计图;
(4)某班主任对学生进行了纪律教育,要求小明和小军分别从题中所述的四个层次中随机选择一个层次说明惩戒内容.请用列表法或画树状图法求两人选择不同教育惩戒层次的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘船由A港沿北偏东60°方向航行20km至B港,然后再沿北偏西30°方向航行20km至C港.
(1)求A,C两港之间的距离;(结果保留到0.1km)
(2)确定C港在A港的什么方向(参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)
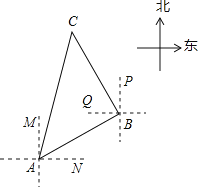
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将函数![]() 的图象沿y轴向上平移得到一条新函数的图象,其中点A(-4,m),B(-1,n),平移后的对应点分别为点A'、B'.若曲线段AB扫过的面积为9(图中的阴影部分),则新图象的函数表达式是 ( )
的图象沿y轴向上平移得到一条新函数的图象,其中点A(-4,m),B(-1,n),平移后的对应点分别为点A'、B'.若曲线段AB扫过的面积为9(图中的阴影部分),则新图象的函数表达式是 ( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
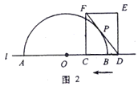
【题目】如图1,点![]() 和矩形
和矩形![]() 的边
的边![]() 都在直线
都在直线![]() 上,以点
上,以点![]() 为圆心,以24为半径作半圆,分别交直线
为圆心,以24为半径作半圆,分别交直线![]() 于
于![]() 两点.已知:
两点.已知: ![]() ,
,![]() ,矩形自右向左在直线
,矩形自右向左在直线![]() 上平移,当点
上平移,当点![]() 到达点
到达点![]() 时,矩形停止运动.在平移过程中,设矩形对角线
时,矩形停止运动.在平移过程中,设矩形对角线![]() 与半圆
与半圆![]() 的交点为
的交点为![]() (点
(点![]() 为半圆上远离点
为半圆上远离点![]() 的交点).
的交点).
(1)如图2,若![]() 与半圆
与半圆![]() 相切,求
相切,求![]() 的值;
的值;
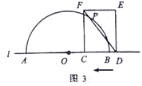
(2)如图3,当![]() 与半圆
与半圆![]() 有两个交点时,求线段
有两个交点时,求线段![]() 的取值范围;
的取值范围;
(3)若线段![]() 的长为20,直接写出此时
的长为20,直接写出此时![]() 的值.
的值.
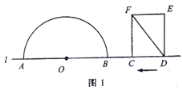
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 与x轴相交于不同的两点
与x轴相交于不同的两点![]() ,
,
(1)求![]() 的取值范围
的取值范围
(2)证明该抛物线一定经过非坐标轴上的一点![]() ,并求出点
,并求出点![]() 的坐标;
的坐标;
(3)当![]() 时,由(2)求出的点
时,由(2)求出的点![]() 和点
和点![]() 构成的
构成的![]() 的面积是否有最值,若有,求出最值及相对应的
的面积是否有最值,若有,求出最值及相对应的![]() 值;若没有,请说明理由.
值;若没有,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com