
 ���õ��������ķ��Ȳ���ʹ����PTC���Ȳ��ϣ����ĵ���R��k�������¶�t���棩����һ����Χ�ڣ��仯�Ĵ���ͼ����ͼ��ʾ��ͨ����Ȳ��ϵ��¶���������10��������30��Ĺ����У��������¶ȳɷ�������ϵ�������¶ȴﵽ30��ʱ�������½�����Сֵ�����������¶����߶����ӣ��¶�ÿ����1�棬��������$\frac{4}{15}$k����
���õ��������ķ��Ȳ���ʹ����PTC���Ȳ��ϣ����ĵ���R��k�������¶�t���棩����һ����Χ�ڣ��仯�Ĵ���ͼ����ͼ��ʾ��ͨ����Ȳ��ϵ��¶���������10��������30��Ĺ����У��������¶ȳɷ�������ϵ�������¶ȴﵽ30��ʱ�������½�����Сֵ�����������¶����߶����ӣ��¶�ÿ����1�棬��������$\frac{4}{15}$k�������� ��1�����ϵΪR=$\frac{k}{t}$������10��6��������k��
��2����t=30������ϵʽ����R�����������R=R��+$\frac{4}{15}$��t-30����
��3����R=6����R=R��+$\frac{4}{15}$��t-30�����t��
��� �⣺��1�����¶���������10��������30��Ĺ����У��������¶ȳɷ�������ϵ��
�����R��t֮��Ĺ�ϵʽΪR=$\frac{k}{t}$��
����10��6��������ʽ�еã�6=$\frac{k}{10}$��
k=60��
�ʵ�10��t��30ʱ��R=$\frac{60}{t}$��
��2����t=30�������ʽ�еã�R=$\frac{60}{30}$��R=2��
���¶���30��ʱ������R=2��k������
�����¶ȴﵽ30��ʱ�������½�����Сֵ�����������¶����߶����ӣ��¶�ÿ����1�棬��������$\frac{4}{15}$k����
�൱t��30ʱ��
R=2+$\frac{4}{15}$��t-30��=$\frac{4}{15}$t-6��
��3����R=5��k����������R=$\frac{4}{15}$t-6�ã�t=41.25���棩��
��R=5����R=$\frac{60}{t}$�����t=12��
���ԣ��¶���12�桫41.25��ʱ�����費����5k����
���� ��Ҫ�����˷�����������Ӧ�ã�����Ĺؼ��Ǹ���ʵ�������г�������ϵʽ����ʵ���������ҵ���Ӧ�ı�����ֵ�����ô���ϵ���������������ʽ���ٸ����Ա�����ֵ�����Ӧ�ĺ���ֵ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
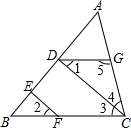 ��ͼ�����������У��ܵõ�DG��BC���ǣ�������
��ͼ�����������У��ܵõ�DG��BC���ǣ�������| A�� | CD��AB��EF��AB | B�� | ��1=��2 | ||
| C�� | ��1=��2����4+��5=180�� | D�� | CD��AB��EF��AB����1=��2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
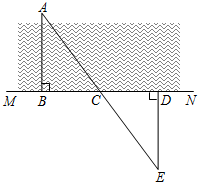 ����ѧ�ۺ�ʵ������ϣ�����ʦ���˸��С���ֱ�����ǰ�һ����Ƥ��һ����������ͼ��ʾС�ӵĿ��ȣ�AΪ�Ӱ���һ����������Сӱ���������ģ�
����ѧ�ۺ�ʵ������ϣ�����ʦ���˸��С���ֱ�����ǰ�һ����Ƥ��һ����������ͼ��ʾС�ӵĿ��ȣ�AΪ�Ӱ���һ����������Сӱ���������ģ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com