
【题目】下列六种说法正确的个数是( )
①无限小数都是无理数;
②正数、负数统称实数;
③无理数的相反数还是无理数;
④无理数与无理数的和一定还是无理数;
⑤无理数与有理数的和一定是无理数;
⑥无理数与有理数的积一定仍是无理数.
A.1
B.2
C.3
D.4
【答案】B
【解析】解:①无限不循环小数都是无理数,故①错误;
②正实数、零、负实数统称实数,故②错误;
③无理数的相反数还是无理数,故③正确;
④无理数与无理数的和可能是无理数、有理数,如﹣π+(π+2)=2,故④错误;
⑤无理数与有理数的和是无理数,如﹣π+2=2﹣π,故⑤正确;
⑥无理数与有理数的积可能是有理数无理数,如0× ![]() =0,故⑥错误;
=0,故⑥错误;
故选:B.
【考点精析】认真审题,首先需要了解无理数(在理解无理数时,要抓住“无限不循环”这个要点,归纳起来有四类:(1)开方开不尽的数;(2)有特定意义的数,如圆周率π,或化简后含有π的数;(3)有特定结构的数,如0.1010010001…等;(4)某些三角函数,如sin60o等).


科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,E,F分别是AB,CD的中点,G,H分别是AF,CE的中点,连结EG,FH. 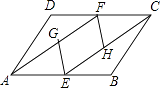
(1)四边形EHFG是不是平行四边形?如果是,请给出证明;如果不是,请说明理由;
(2)求四边形EHFG的面积与平行四边形ABCD的面积之比.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店需要购进甲、乙两种商品共180件,其进价和售价如表:(注:获利=售价﹣进价)
甲 | 乙 | |
进价(元/件) | 14 | 35 |
售价(元/件) | 20 | 43 |
(1)若商店计划销售完这批商品后能获利1240元,问甲、乙两种商品应分别购进多少件?
(2)若商店计划投入资金少于5040元,且销售完这批商品后获利多于1312元,请问有哪几种购货方案?并直接写出其中获利最大的购货方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
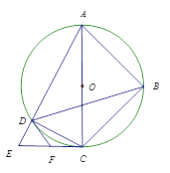
【题目】如图,四边形ABCD内接于⊙O,对角线AC为⊙O的直径,过点C作AC的垂线交AD的延长线于点E,点F为CE的中点,连接DB, DF.
(1)求证:DF是⊙O的切线;
(2)若DB平分∠ADC,AB=a, ![]() ∶DE=4∶1,写出求DE长的思路.
∶DE=4∶1,写出求DE长的思路.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面的证明. 已知:如图,BE∥CD,∠A=∠1,
求证:∠C=∠E.
证明:∵BE∥CD (已知 )
∴∠2=∠C ()
又∵∠A=∠1 (已知 )
∴AC∥DE ()
∴∠2=∠E ()
∴∠C=∠E (等量代换 )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A、C的坐标分别为(﹣4,4),(﹣1,2).
(1)①请在如图所示的网格平面内作出平面直角坐标系;
②将△ABC向右平移2个单位长度,然后再向下平移3个单位长度,得到△A′B′C′,画出平移后的△A′B′C′.
(2)写出点△A′B′C′各个顶点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将等边△ABC绕点C顺时针旋转120°得到△EDC,连接AD,BD.则下列结论:
①AC=AD;②BD⊥AC;③四边形ACED是菱形.
其中正确的个数是( )

A.0 B.1 C.2 D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com