
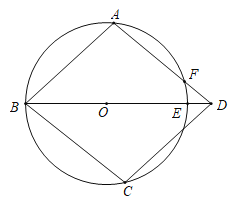
【题目】如图,在⊙O上依次有A、B、C三点,BO的延长线交⊙O于E,![]() ,过点C作CD∥AB交BE的延长线于D,连AD交⊙O于点F.
,过点C作CD∥AB交BE的延长线于D,连AD交⊙O于点F.
(1)求证:四边形ABCD是菱形;
(2)连接OA、OF.
①当∠ABC= °时,点F为![]() 的中点;
的中点;
②若∠AOF=3∠FOE且AF=3,则⊙O的半径是 .
【答案】(1)证明见解析;(2)①72;②3.
【解析】
(1)先根据圆的性质得:∠CBD=∠ABD,由平行线的性质得:∠ABD=∠CDB,根据直径和等式的性质得![]() ,则AB=BC,即可得出结论;
,则AB=BC,即可得出结论;
(2)①由题意得出∠AOF=∠EOF=m,证出∠ABE=∠ADE=m,则∠OAF=∠OFA=∠EOF+∠ADE=2m,由三角形内角和定理得出方程,解方程即可;
②先设∠FOE=x,则∠AOF=3x,根据∠ABC+∠BAD=180°,列方程求出x的值,证△AOF是等边三角形,得出OF=AF=3即可.
(1)证明:∵![]() ,
,
∴∠CBD=∠ABD,
∵CD∥AB,
∴∠ABD=∠CDB,
∴∠CBD=∠CDB,
∴CB=CD,
∵BE是⊙O的直径,
∴![]() ,
,
∴AB=BC=CD,
∵CD∥AB,
∴四边形ABCD是菱形;
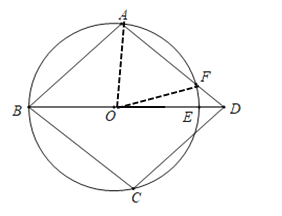
(2)解:如图所示:
①F为![]() 的中点,则∠AOF=∠EOF,
的中点,则∠AOF=∠EOF,
设∠AOF=∠EOF=m,
∵四边形ABCD是菱形,
∴AB=AD,∠ABE=∠ADE,
∵∠AOD=2∠ABE,
∴∠ABE=∠ADE=m,
∴∠OAF=∠OFA=∠EOF+∠ADE=2m,
∵∠AOF+∠OAF+∠OFA=180°,
∴2m+2m+m=180°,
∴m=36°,
∴∠ABE=72°,
即∠ABC=72°时,点F为![]() 的中点,
的中点,
故答案为:72;
②∵∠AOF=3∠FOE,
设∠FOE=x,则∠AOF=3x,
∠AOD=∠FOE+∠AOF=4x,
∵OA=OF,
∴∠OAF=∠OFA=![]() (180°﹣3x),
(180°﹣3x),
∵OA=OB,
∴∠OAB=∠OBA=2x,
∴∠ABC=4x,
∵BC∥AD,
∴∠ABC+∠BAD=180°,
∴4x+2x+![]() (180°﹣3x)=180°,
(180°﹣3x)=180°,
解得:x=20°,
∴∠AOF=3x=60°,
∵OA=OF,
∴△AOF是等边三角形,
∴OF=AF=3,
即⊙O的半径是3;
故答案为:3.
【点晴】
本题考查平行四边形和菱形的判定和性质,等边三角形的判定和性质,圆周角定理等知识,解题的关键是学会设未知数,列方程求角的度数,证明三角形是等边三角形是解题的突破点,是属于中考常考题型.


科目:初中数学 来源: 题型:
【题目】哈市红十字预计在2019年儿童节前为郊区某小学发放学习用品,联系某工厂加工学习用品.机器每小时加工产品的数量比手工每小时加工产品的数量的2倍多9件,若加工1800件这样的产品,机器加工所用的时间是手工加工所用时间的![]() 倍.
倍.
(1)求手工每小时加工产品的数量;
(2)经过调查该小学的小学生的总数不超过1332名,每名小学生分发两个学习用品,工厂领导打算在两天内(48小时)完成任务,打算以机器加工为主,同时人工也参与加工(人工与机器加工不能同时进行),为了保证按时完成加工任务,人工至少要加工多少小时?
查看答案和解析>>
科目:初中数学 来源: 题型:
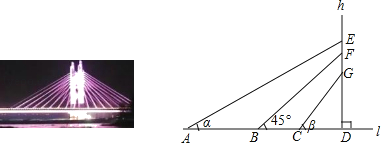
【题目】如图,是一座横跨沙颖河的斜拉桥,拉索两端分别固定在主梁l和索塔h上,索塔h垂直于主梁l,垂足为D.拉索AE,BF,CG的仰角分别是α,45°,β,且α+β=90°(α<β),AB=15m,BC=5m,CD=4m,EF=3FG,求拉索AE的长.(精确到1m,参考数据:![]() ≈2.24,
≈2.24,![]() ≈1.41)
≈1.41)
查看答案和解析>>
科目:初中数学 来源: 题型:
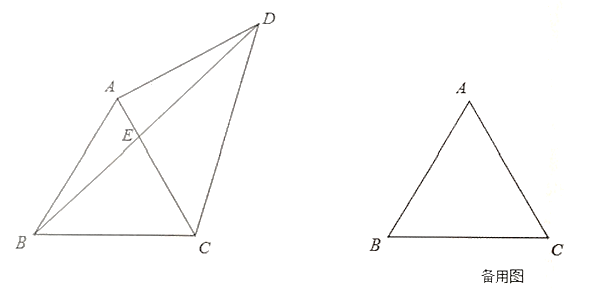
【题目】如图,![]() 是边长为2的等边三角形,点
是边长为2的等边三角形,点![]() 与点
与点![]() 分别位于直线
分别位于直线![]() 的两侧,且
的两侧,且![]() ,连接
,连接![]() ,
,![]() 交直线
交直线![]() 于点
于点![]() .
.
(1)当![]() 时,求线段
时,求线段![]() 的长;
的长;
(2)过点![]() 作
作![]() ,垂足为点
,垂足为点![]() ,直线
,直线![]() 交
交![]() 于点
于点![]() ,
,
①当![]() 时,设
时,设![]() (其中
(其中![]() 表示
表示![]() 的面积,
的面积,![]() 表示
表示![]() 的面积),求
的面积),求![]() 关于
关于![]() 的函数关系式,并写出
的函数关系式,并写出![]() 的取值范围;
的取值范围;
②当![]() 时,请直接写出线段
时,请直接写出线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 与x轴交于点A,与y轴交于点B,直线
与x轴交于点A,与y轴交于点B,直线![]() 与x轴交于点C.
与x轴交于点C.

(1)求点B的坐标;
(2)横、纵坐标都是整数的点叫做整点.记线段![]() 围成的区域(不含边界)为G.
围成的区域(不含边界)为G.
①当![]() 时,结合函数图象,求区域G内整点的个数;
时,结合函数图象,求区域G内整点的个数;
②若区域G内恰有2个整点,直接写出k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,![]() 为原点,抛物线
为原点,抛物线![]() 经过
经过![]() 三点,且其对称轴为
三点,且其对称轴为![]() 其中点
其中点![]() ,点
,点![]() .
.
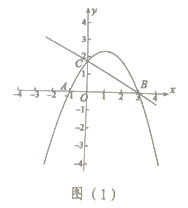
(1)求抛物线的解析式;
(2)①如图(1),点![]() 是直线
是直线![]() 上方抛物线上的动点,当四边形
上方抛物线上的动点,当四边形![]() 的面积取最大值时,求点
的面积取最大值时,求点![]() 的坐标;
的坐标;
②如图(2),连接![]() 在抛物线上有一点
在抛物线上有一点![]() 满足
满足![]() ,请直接写出点
,请直接写出点![]() 的横坐标.
的横坐标.
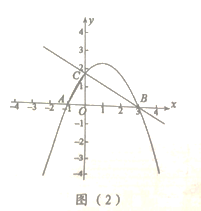
查看答案和解析>>
科目:初中数学 来源: 题型:
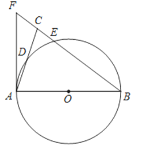
【题目】如图,在△ABC中,BA=BC,以AB为直径的⊙O分别交AC,BC于点D,E,BC的延长线与⊙O的切线AF交于点F.
(1)求证:∠ABC=2∠CAF;
(2)若AC=2![]() ,CE:EB=1:4,求CE,AF的长.
,CE:EB=1:4,求CE,AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
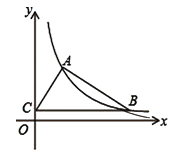
【题目】已知:如图,第一象限内的点A,B在反比例函数的图象上,点C在y轴上,BC∥x轴,点A的坐标为(2,4),且tan∠ACB=![]()
求:(1)反比例函数的解析式;
(2)点C的坐标;
(3)∠ABC的余弦值.
查看答案和解析>>
科目:初中数学 来源: 题型:
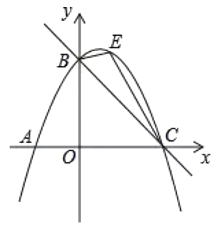
【题目】如图,直线![]() 与 x 轴交于点 C,与 y 轴交于点 B,抛物线
与 x 轴交于点 C,与 y 轴交于点 B,抛物线 ![]() 经过 B、C 两点.
经过 B、C 两点.
(1)求抛物线的解析式;
(2)如图,点 E 是抛物线上的一动点(不与 B,C 两点重合),△BEC 面积记为 S,当 S 取何值时,对应的点 E 有且只有三个?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com